用变分推断统一理解生成模型(VAE、GAN、AAE、ALI)
By 苏剑林 | 2018-07-18 | 456969位读者 |前言:我小学开始就喜欢纯数学,后来也喜欢上物理,还学习过一段时间的理论物理,直到本科毕业时,我才慢慢进入机器学习领域。所以,哪怕在机器学习领域中,我的研究习惯还保留着数学和物理的风格:企图从最少的原理出发,理解、推导尽可能多的东西。这篇文章是我这个理念的结果之一,试图以变分推断作为出发点,来统一地理解深度学习中的各种模型,尤其是各种让人眼花缭乱的GAN。本文已经挂到arxiv上,需要读英文原稿的可以移步到《Variational Inference: A Unified Framework of Generative Models and Some Revelations》。
下面是文章的介绍。其实,中文版的信息可能还比英文版要稍微丰富一些,原谅我这蹩脚的英语...
摘要:本文从一种新的视角阐述了变分推断,并证明了EM算法、VAE、GAN、AAE、ALI(BiGAN)都可以作为变分推断的某个特例。其中,论文也表明了标准的GAN的优化目标是不完备的,这可以解释为什么GAN的训练需要谨慎地选择各个超参数。最后,文中给出了一个可以改善这种不完备性的正则项,实验表明该正则项能增强GAN训练的稳定性。
近年来,深度生成模型,尤其是GAN,取得了巨大的成功。现在我们已经可以找到数十个乃至上百个GAN的变种。然而,其中的大部分都是凭着经验改进的,鲜有比较完备的理论指导。
本文的目标是通过变分推断来给这些生成模型建立一个统一的框架。首先,本文先介绍了变分推断的一个新形式,这个新形式其实在博客以前的文章中就已经介绍过,它可以让我们在几行字之内导出变分自编码器(VAE)和EM算法。然后,利用这个新形式,我们能直接导出GAN,并且发现标准GAN的loss实则是不完备的,缺少了一个正则项。如果没有这个正则项,我们就需要谨慎地调整超参数,才能使得模型收敛。
实际上,本文这个工作的初衷,就是要将GAN纳入到变分推断的框架下。目前看来,最初的意图已经达到了,结果让人欣慰。新导出的正则项实际上是一个副产品,并且幸运的是,在我们的实验中这个副产品生效了。
变分推断新解 #
假设$x$为显变量,$z$为隐变量,$\tilde{p}(x)$为$x$的证据分布,并且有
$$\begin{equation}q(x)=q_{\theta}(x)=\int q_{\theta}(x,z)dz\end{equation}$$
我们希望$q_{\theta}(x)$能逼近$\tilde{p}(x)$,所以一般情况下我们会去最大化似然函数
$$\begin{equation}\theta = \mathop{\text{argmax}}_{\theta}\, \int \tilde{p}(x)\log q(x) dx\end{equation}$$
这也等价于最小化KL散度$KL(\tilde{p}(x)\Vert q(x))$:
$$\begin{equation}KL(\tilde{p}(x)\Vert q(x)) = \int \tilde{p}(x) \log \frac{\tilde{p}(x)}{q(x)}dx\end{equation}$$
但是由于积分可能难以计算,因此大多数情况下都难以直接优化。
变分推断中,首先引入联合分布$p(x,z)$使得$\tilde{p}(x)=\int p(x,z)dz$,而变分推断的本质,就是将边际分布的KL散度$KL(\tilde{p}(x)\Vert q(x))$改为联合分布的KL散度$KL(p(x,z)\Vert q(x,z))$或$KL(q(x,z)\Vert p(x,z))$,而
$$\begin{equation}\begin{aligned}KL(p(x,z)\Vert q(x,z)) &= KL(\tilde{p}(x)\Vert q(x)) + \int \tilde{p}(x) KL(p(z|x)\Vert q(z|x)) dx\\
&\geq KL(\tilde{p}(x)\Vert q(x))\end{aligned}\end{equation}$$
意味着联合分布的KL散度是一个更强的条件(上界)。所以一旦优化成功,那么我们就得到$q(x,z)\to p(x,z)$,从而$\int q(x,z)dz \to \int p(x,z)dz = \tilde{p}(x)$,即$\int q(x,z)dz$成为了真实分布$\tilde{p}(x)$的一个近似。
当然,我们本身不是为了加强条件而加强,而是因为在很多情况下,$KL(p(x,z)\Vert q(x,z))$或$KL(q(x,z)\Vert p(x,z))$往往比$KL(\tilde{p}(x)\Vert q(x))$更加容易计算。所以变分推断是提供了一个可计算的方案。
VAE和EM算法 #
由上述关于变分推断的新理解,我们可以在几句话内导出两个基本结果:变分自编码器和EM算法。这部分内容,实际上在《从最大似然到EM算法:一致的理解方式》和《变分自编码器(二):从贝叶斯观点出发》已经详细介绍过了。这里用简单几句话重提一下。
VAE #
在VAE中,我们设$q(x,z)=q(x|z)q(z), p(x,z)=\tilde{p}(x) p(z|x)$,其中$q(x|z),p(z|x)$带有未知参数的高斯分布而$q(z)$是标准高斯分布。最小化的目标是
$$\begin{equation}\label{eq:kl-oo}KL\left(p(x,z)\Vert q(x,z) \right)=\iint \tilde{p}(x) p(z|x) \log \frac{\tilde{p}(x) p(z|x)}{q(x|z)q(z)}dxdz\end{equation}$$
其中$\log \tilde{p}(x)$没有包含优化目标,可以视为常数,而对$\tilde{p}(x)$的积分则转化为对样本的采样,从而
$$\begin{equation}\mathbb{E}_{x\sim \tilde{p}(x)}\left[-\int p(z|x)\log q(x|z)dz + KL(p(z|x)\Vert q(z))\right]\end{equation}$$
因为$q(x|z),p(z|x)$为带有神经网络的高斯分布,这时候$KL\left(p(z|x)\Vert q(z)\right)$可以显式地算出,而通过重参数技巧来采样一个点完成积分$\int p(z|x) \log q(x|z)dz$的估算,可以得到VAE最终要最小化的loss:
$$\begin{equation}\mathbb{E}_{x\sim \tilde{p}(x)}\Big[-\log q(x|z) + KL(p(z|x)\Vert q(z))\Big]\end{equation}$$
EM算法 #
在VAE中我们对后验分布做了约束,仅假设它是高斯分布,所以我们优化的是高斯分布的参数。如果不作此假设,那么直接优化原始目标$\eqref{eq:kl-oo}$,在某些情况下也是可操作的,但这时候只能采用交替优化的方式:先固定$p(z|x)$,优化$q(x|z)$,那么就有
$$\begin{equation}\label{eq:em-1}q(x|z) = \mathop{\text{argmax}}_{q(x|z)} \,\mathbb{E}_{x\sim \tilde{p}(x)}\left[\int p(z|x) \log q(x,z) dz\right]\end{equation}$$
完成这一步后,我们固定$q(x,z)$,优化$p(z|x)$,先将$q(x|z)q(z)$写成$q(z|x)q(x)$的形式:
$$\begin{equation}q(x)=\int q(x|z)q(z)dz,\quad q(z|x)=\frac{q(x|z)q(z)}{q(x)}\end{equation}$$
那么有
$$\begin{equation}\begin{aligned}p(z|x) =& \mathop{\text{argmin}}_{p(z|x)} \,\mathbb{E}_{x\sim \tilde{p}(x)}\left[\int p(z|x) \log \frac{p(z|x)}{q(z|x)q(x)} dz\right]\\
=& \mathop{\text{argmin}}_{p(z|x)} \,\mathbb{E}_{x\sim \tilde{p}(x)}\left[KL\left(p(z|x)\Vert q(z|x)\right)-\log q(x)\right]\\
=& \mathop{\text{argmin}}_{p(z|x)} \,\mathbb{E}_{x\sim \tilde{p}(x)} \left[KL\left(p(z|x)\Vert q(z|x)\right)\right]
\end{aligned}\end{equation}$$
由于现在对$p(z|x)$没有约束,因此可以直接让$p(z|x)=q(z|x)$使得loss等于0。也就是说,$p(z|x)$有理论最优解:
$$\begin{equation}\label{eq:em-2}p(z|x) = \frac{q(x|z)q(z)}{\int q(x|z)q(z)dz}\end{equation}$$
$\eqref{eq:em-1},\eqref{eq:em-2}$的交替执行,构成了EM算法的求解步骤。这样,我们从变分推断框架中快速得到了EM算法。
变分推断下的GAN #
在这部分内容中,我们介绍了一般化的将GAN纳入到变分推断中的方法,这将引导我们得到GAN的新理解,以及一个有效的正则项。
一般框架 #
同VAE一样,GAN也希望能训练一个生成模型$q(x|z)$,来将$q(z)=N(z;0,I)$映射为数据集分布$\tilde{p}(x)$,不同于VAE中将$q(x|z)$选择为高斯分布,GAN的选择是
$$\begin{equation}q(x|z)=\delta\left(x - G(z)\right),\quad q(x)=\int q(x|z)q(z)dz\end{equation}$$
其中$\delta(x)$是狄拉克$\delta$函数,$G(z)$即为生成器的神经网络。
一般我们会认为$z$是一个隐变量,但由于$\delta$函数实际上意味着单点分布,因此可以认为$x$与$z$的关系已经是一一对应的,所以$z$与$x$的关系已经“不够随机”,在GAN中我们认为它不是隐变量(意味着我们不需要考虑后验分布$p(z|x)$)。
事实上,在GAN中仅仅引入了一个二元的隐变量$y$来构成联合分布
$$\begin{equation}q(x,y)=\left\{\begin{aligned}&\tilde{p}(x)p_1,\,y=1\\&q(x)p_0,\,y=0\end{aligned}\right.\end{equation}$$
这里$p_1 = 1-p_0$描述了一个二元概率分布,我们直接取$p_1=p_0=1/2$。另一方面,我们设$p(x,y)=p(y|x) \tilde{p}(x)$,$p(y|x)$是一个条件伯努利分布。而优化目标是另一方向的$KL\left(q(x,y)\Vert p(x,y) \right)$:
$$\begin{equation}\begin{aligned}KL\left(q(x,y)\Vert p(x,y) \right)=&\int \tilde{p}(x)p_1\log \frac{\tilde{p}(x)p_1}{p(1|x)\tilde{p}(x)}dx+\int q(x)p_0\log \frac{q(x)p_0}{p(0|x)\tilde{p}(x)}dx\\
\sim&\int \tilde{p}(x)\log \frac{1}{p(1|x)}dx+\int q(x)\log \frac{q(x)}{p(0|x)\tilde{p}(x)}dx\end{aligned}\end{equation}$$
一旦成功优化,那么就有$q(x,y)\to p(x,y)$,那么
$$\begin{equation}p_1 \tilde{p}(x) + p_0 q(x) = \sum_y q(x,y) \to \sum_y p(x,y) = \tilde{p}(x)\end{equation}$$
从而$q(x)\to\tilde{p}(x)$,完成了生成模型的构建。
现在我们优化对象有$p(y|x)$和$G(x)$,记$p(1|x)=D(x)$,这就是判别器。类似EM算法,我们进行交替优化:先固定$G(z)$,这也意味着$q(x)$固定了,然后优化$p(y|x)$,这时候略去常量,得到优化目标为:
$$\begin{equation}D = \mathop{\text{argmin}}_{D} -\mathbb{E}_{x\sim\tilde{p}(x)}\left[\log D(x)\right]-\mathbb{E}_{x\sim q(x)}\left[\log (1-D(x))\right]\end{equation}$$
然后固定$D(x)$来优化$G(x)$,这时候相关的loss为:
$$\begin{equation}\label{eq:gan-g-loss}G = \mathop{\text{argmin}}_{G}\int q(x)\log \frac{q(x)}{(1-D(x)) \tilde{p}(x)}dx\end{equation}$$
这里包含了我们不知道的$\tilde{p}(x)$,但是假如$D(x)$模型具有足够的拟合能力,那么跟$\eqref{eq:em-2}$式同理,$D(x)$的最优解应该是
$$\begin{equation}D(x)=\frac{\tilde{p}(x)}{\tilde{p}(x)+q^{o}(x)}\end{equation}$$
这里的$q^{o}(x)$是前一阶段的$q(x)$。从中解出$\tilde{p}(x)$,代入$\eqref{eq:gan-g-loss}$得到
$$\begin{equation}\begin{aligned}\int q(x)\log \frac{q(x)}{D(x) q^{o}(x)}dx=&-\mathbb{E}_{x\sim q(x)}\log D(x) + KL\left(q(x)\Vert q^{o}(x)\right)\\
=&-\mathbb{E}_{z\sim q(z)}\log D(G(z)) + KL\left(q(x)\Vert q^{o}(x)\right)
\end{aligned}\end{equation}$$
基本分析 #
可以看到,第一项就是标准的GAN生成器所采用的loss之一。
$$\begin{equation}-\mathbb{E}_{z\sim q(z)}\log D(G(z))\end{equation}$$
多出来的第二项,描述了新分布与旧分布之间的距离。这两项loss是对抗的,因为$KL\left(q(x)\Vert q^{o}(x)\right)$希望新旧分布尽量一致,但是如果判别器充分优化的话,对于旧分布$q^{o}(x)$中的样本,$D(x)$都很小(几乎都被识别为负样本),所以$-\log D(x)$会相当大,反之亦然。这样一来,整个loss一起优化的话,模型既要“传承”旧分布$q^{o}(x)$,同时要在往新方向$p(1|y)$探索,在新旧之间插值。
我们知道,目前标准的GAN的生成器loss都不包含$KL\left(q(x)\Vert q^{o}(x)\right)$,这事实上造成了loss的不完备。假设有一个优化算法总能找到$G(z)$的理论最优解、并且$G(z)$具有无限的拟合能力,那么$G(z)$只需要生成唯一一个使得$D(x)$最大的样本(不管输入的$z$是什么),这就是模型坍缩。这样说的话,理论上它一定会发生。
那么,$KL\left(q(x)\Vert q^{o}(x)\right)$给我们的启发是什么呢?我们设
$$\begin{equation}q^{o}(x)=q_{\theta-\Delta \theta}(x),\quad q(x)=q_{\theta}(x)\end{equation}$$
也就是说,假设当前模型的参数改变量为$\Delta\theta$,那么展开到二阶得到
$$\begin{equation}KL\left(q(x)\Vert q^{o}(x)\right)\approx \int\frac{\left(\Delta\theta\cdot \nabla_{\theta}q_{\theta}(x)\right)^2}{2q_{\theta}(x)} dx \approx \left(\Delta\theta\cdot c\right)^2\end{equation}$$
我们已经指出一个完备的GAN生成器的损失函数应该要包含$KL\left(q(x)\Vert q^{o}(x)\right)$,如果不包含的话,那么就要通过各种间接手段达到这个效果,上述近似表明额外的损失约为$\left(\Delta\theta\cdot c\right)^2$,这就要求我们不能使得它过大,也就是不能使得$\Delta\theta$过大(在每个阶段$c$可以近似认为是一个常数)。而我们用的是基于梯度下降的优化算法,所以$\Delta\theta$正比于梯度,因此标准GAN训练时的很多trick,比如梯度裁剪、用adam优化器、用BN,都可以解释得通了,它们都是为了稳定梯度,使得$\theta$不至于过大,同时,$G(z)$的迭代次数也不能过多,因为过多同样会导致$\Delta\theta$过大。
还有,这部分的分析只适用于生成器,而判别器本身并不受约束,因此判别器可以训练到最优。
正则项 #
现在我们从中算出一些真正有用的内容,直接对$KL\left(q(x)\Vert q^{o}(x)\right)$进行估算,以得到一个可以在实际训练中使用的正则项。直接计算是难以进行的,但我们可以用$KL\left(q(x,z)\Vert \tilde{q}(x,z)\right)$去估算它:
$$\begin{equation}\begin{aligned}KL\left(q(x,z)\Vert \tilde{q}(x,z)\right)=&\iint q(x|z)q(z)\log \frac{q(x|z)q(z)}{\tilde{q}(x|z)q(z)}dxdz\\
=&\iint \delta\left(x-G(z)\right)q(z)\log \frac{\delta\left(x-G(z)\right)}{\delta\left(x-G^{o}(z)\right)}dxdz\\
=&\int q(z)\log \frac{\delta(0)}{\delta\left(G(z)-G^{o}(z)\right)}dz
\end{aligned}\end{equation}$$
因为有极限
$$\begin{equation}\delta(x)=\lim_{\sigma\to 0}\frac{1}{(2\pi\sigma^2)^{d/2}}\exp\left(-\frac{x^2}{2\sigma^2}\right)\end{equation}$$
所以可以将$\delta(x)$看成是小方差的高斯分布,代入算得也就是我们有
$$\begin{equation}KL\left(q(x)\Vert q^{o}(x)\right)\sim \lambda \int q(z)\Vert G(z) - G^{o}(z)\Vert^2 dz\end{equation}$$
所以完整生成器的loss可以选为
$$\begin{equation}\mathbb{E}_{z\sim q(z)}\left[-\log D(G(z))+\lambda \Vert G(z) - G^{o}(z)\Vert^2\right] \end{equation}$$
也就是说,可以用新旧生成样本的距离作为正则项,正则项保证模型不会过于偏离旧分布。
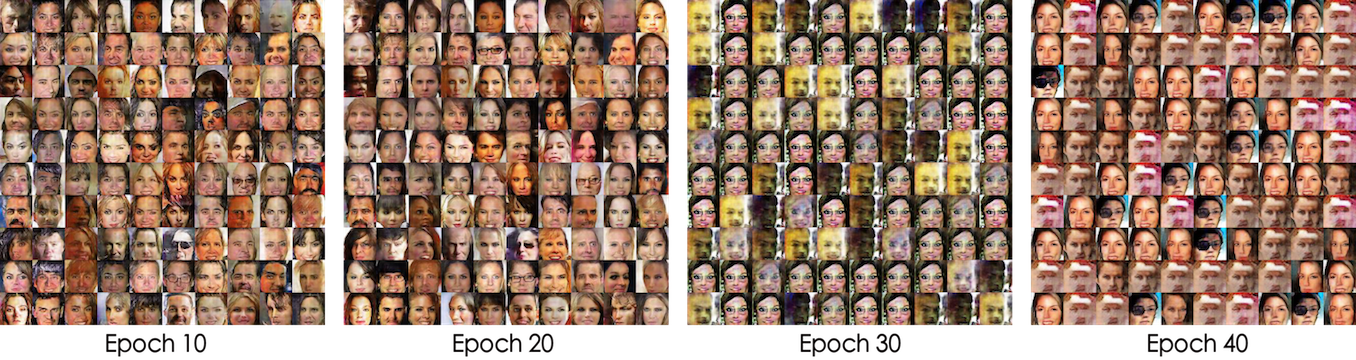
下面的两个在人脸数据CelebA上的实验表明这个正则项是生效的。实验代码修改自这里,目前放在我的github上。
实验一:普通的DCGAN网络,每次迭代生成器和判别器各训练一个batch。
实验二:普通的DCGAN网络,但去掉BN,每次迭代生成器和判别器各训练五个batch。
GAN相关模型 #
对抗自编码器(Adversarial Autoencoders,AAE)和对抗推断学习(Adversarially Learned Inference,ALI)这两个模型是GAN的变种之一,也可以被纳入到变分推断中。当然,有了前述准备后,这仅仅就像两道作业题罢了。
有意思的是,在ALI之中,我们有一些反直觉的结果。
GAN视角下的AAE #
事实上,只需要在GAN的论述中,将$x,z$的位置交换,就得到了AAE的框架。
具体来说,AAE希望能训练一个编码模型$p(z|x)$,来将真实分布$\tilde{q}(x)$映射为标准高斯分布$q(z)=N(z;0,I)$,而
$$\begin{equation}p(z|x)=\delta\left(z - E(x)\right),\quad p(z)=\int p(z|x)\tilde{q}(x)dx\end{equation}$$
其中$E(x)$即为编码器的神经网络。
同GAN一样,AAE引入了一个二元的隐变量$y$,并有
$$\begin{equation}p(z,y)=\left\{\begin{aligned}&p(z)p_1,\,y=1\\&q(z)p_0,\,y=0\end{aligned}\right.\end{equation}$$
同样直接取$p_1=p_0=1/2$。另一方面,我们设$q(z,y)=q(y|z) q(z)$,这里的后验分布$p(y|z)$是一个输入为$z$的二元分布,然后去优化$KL\left(p(z,y)\Vert q(z,y) \right)$:
$$\begin{equation}\begin{aligned}KL\left(p(z,y)\Vert q(z,y) \right)=&\int p(z)p_1\log \frac{p(z)p_1}{q(1|z)q(z)}dz+\int q(z)p_0\log \frac{q(z)p_0}{q(0|z)q(z)}dz\\
\sim&\int p(z)\log \frac{p(z)}{q(1|z)q(z)}dz+\int q(z)\log \frac{1}{q(0|z)}dz\end{aligned}\end{equation}$$
现在我们优化对象有$q(y|z)$和$E(x)$,记$q(0|z)=D(z)$,依然交替优化:先固定$E(x)$,这也意味着$p(z)$固定了,然后优化$q(y|z)$,这时候略去常量,得到优化目标为:
$$\begin{equation}\begin{aligned}D=\mathop{\text{argmin}}_D &-\mathbb{E}_{z\sim p(z)}\left[\log (1-D(z))\right]-\mathbb{E}_{z\sim q(z)}\left[\log D(z)\right]\\
=\mathop{\text{argmin}}_D &-\mathbb{E}_{z\sim \tilde{p}(x)}\left[\log (1-D(E(x)))\right]-\mathbb{E}_{z\sim q(z)}\left[\log D(z)\right]\end{aligned}\end{equation}$$
然后固定$D(z)$来优化$E(x)$,这时候相关的loss为:
$$\begin{equation}E = \mathop{\text{argmin}}_E \int p(z)\log \frac{p(z) }{(1-D(z)) q(z)}dz\end{equation}$$
利用$D(z)$的理论最优解$D(z)=q(z)/[p^{o}(z)+q(z)]$,代入loss得到
$$\begin{equation}\mathbb{E}_{x\sim \tilde{p}(x)}[-\log D(E(x))] + KL\left(p(z)\Vert p^{o}(z)\right)\end{equation}$$
一方面,同标准GAN一样,谨慎地训练,我们可以去掉第二项,得到
$$\begin{equation}\mathbb{E}_{x\sim \tilde{p}(x)}[-\log D(E(x))]\end{equation}$$
另外一方面,我们可以得到编码器后再训练一个解码器$G(z)$,但是如果所假设的$E(x),G(z)$的拟合能力是充分的,重构误差可以足够小,那么将$G(z)$加入到上述loss中并不会干扰GAN的训练,因此可以联合训练:
$$\begin{equation}G,E = \mathop{\text{argmin}}_{G,E}\mathbb{E}_{x\sim \tilde{p}(x)}\left[-\log D(E(x))+\lambda\Vert x - G(E(x))\Vert^2\right]\end{equation}$$
反直觉的ALI版本 #
ALI像是GAN和AAE的融合,另一个几乎一样的工作是Bidirectional GAN (BiGAN)。相比于GAN,它将$z$也作为隐变量纳入到变分推断中。具体来说,在ALI中有
$$\begin{equation}q(x,z,y)=\left\{\begin{aligned}&p(z|x)\tilde{p}(x) p_1,\,y=1\\&q(x|z)q(z)p_0,\,y=0\end{aligned}\right.\end{equation}$$
以及$p(x,z,y)=p(y|x,z) p(z|x) \tilde{p}(x)$,然后去优化$KL\left(q(x,z,y)\Vert p(x,z,y) \right)$:
$$\begin{equation}\begin{aligned}&\iint p(z|x)\tilde{p}(x) p_1\log \frac{p(z|x)\tilde{p}(x) p_1}{p(1|x,z) p(z|x) \tilde{p}(x)}dxdz\\
+&\iint q(x|z)q(z)p_0\log \frac{q(x|z)q(z)p_0}{p(0|x,z) p(z|x) \tilde{p}(x)}dxdz\end{aligned}\end{equation}$$
等价于最小化
$$\begin{equation}\label{eq: ori-loss-ali}\iint p(z|x)\tilde{p}(x)\log \frac{1}{p(1|x,z)}dxdz+\iint q(x|z)q(z)\log \frac{q(x|z)q(z)}{p(0|x,z) p(z|x) \tilde{p}(x)}dxdz\end{equation}$$
现在优化的对象有$p(y|x,z),p(z|x),q(x|z)$,记$p(1|x,z)=D(x,z)$,而$p(z|x)$是一个带有编码器$E$的高斯分布或狄拉克分布,$q(x|z)$是一个带有生成器$G$的高斯分布或狄拉克分布。依然交替优化:先固定$E,G$,那么与$D$相关的loss为
$$\begin{equation}D=\mathop{\text{argmin}}_D -\mathbb{E}_{x\sim\tilde{p}(x),z\sim p(z|x)} \log D(x,z) - \mathbb{E}_{z\sim q(z),x\sim q(x|z)} \log (1-D(x,z))\end{equation}$$
跟VAE一样,对$p(z|x)$和$q(x|z)$的期望可以通过“重参数”技巧完成。接着固定$D$来优化$G,E$,因为这时候有$E$又有$G$,整个loss没得化简,还是$\eqref{eq: ori-loss-ali}$那样。但利用$D$的最优解
$$\begin{equation}D(x,z)=\frac{p^{o}(z|x)\tilde{p}(x)}{p^{o}(z|x)\tilde{p}(x)+q^{o}(x|z)q(z)}\end{equation}$$
可以转化为
$$\begin{equation}\begin{aligned}-\iint p(z|x)\tilde{p}(x)\log D(x, z) dxdz -\iint q(x|z) q(z)\log D(x, z) dxdz\\
+\int q(z) KL(q(x|z)\Vert q^o(x|z)) dz + \iint q(x|z) q(z)\log \frac{p^o(z|x)}{p(z|x)}dxdz\end{aligned}\end{equation}$$
由于$q(x|z),p(x|z)$都是高斯分布,事实上后两项我们可以具体地算出来(配合重参数技巧),但同标准GAN一样,谨慎地训练,我们可以简单地去掉后面两项,得到
$$\begin{equation}\label{eq:our-ali-g}-\iint p(z|x)\tilde{p}(x)\log D(x, z) dxdz -\iint q(x|z) q(z)\log D(x, z) dxdz\end{equation}$$
这就是我们导出的ALI的生成器和编码器的loss,它跟标准的ALI结果有所不同。标准的ALI(包括普通的GAN)将其视为一个极大极小问题,所以生成器和编码器的loss为
$$\begin{equation}\label{eq:our-ali-g-o1}\iint p(z|x)\tilde{p}(x)\log D(x, z) dxdz + \iint q(x|z) q(z)\log (1-D(x, z)) dxdz\end{equation}$$
或
$$\begin{equation}\label{eq:our-ali-g-o2}-\iint p(z|x)\tilde{p}(x)\log (1-D(x, z)) dxdz -\iint q(x|z) q(z)\log D(x, z) dxdz\end{equation}$$
它们都不等价于$\eqref{eq:our-ali-g}$。针对这个差异,事实上笔者也做了实验,结果表明这里的ALI有着和标准的ALI同样的表现,甚至可能稍好一些(可能是我的自我良好的错觉,所以就没有放图了)。这说明,将对抗网络视为一个极大极小问题仅仅是一个直觉行为,并非总应该如此。
结论综述 #
本文的结果表明了变分推断确实是一个推导和解释生成模型的统一框架,包括VAE和GAN。通过变分推断的新诠释,我们介绍了变分推断是如何达到这个目的的。
当然,本文不是第一篇提出用变分推断研究GAN这个想法的文章。在《On Unifying Deep Generative Models》一文中,其作者也试图用变分推断统一VAE和GAN,也得到了一些启发性的结果。但笔者觉得那不够清晰。事实上,我并没有完全读懂这篇文章,我不大确定,这篇文章究竟是将GAN纳入到了变分推断中了,还是将VAE纳入到了GAN中~相对而言,我觉得本文的论述更加清晰、明确一些。
看起来变分推断还有很大的挖掘空间,等待着我们去探索。
转载到请包括本文地址:https://kexue.fm/archives/5716
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jul. 18, 2018). 《用变分推断统一理解生成模型(VAE、GAN、AAE、ALI) 》[Blog post]. Retrieved from https://kexue.fm/archives/5716
@online{kexuefm-5716,
title={用变分推断统一理解生成模型(VAE、GAN、AAE、ALI)},
author={苏剑林},
year={2018},
month={Jul},
url={\url{https://kexue.fm/archives/5716}},
}













July 19th, 2018
今天老师上课在讲GAN,突然想到之前读过VAE和GAN统一的论文的介绍(就是文末提到的文献),结果谷歌一搜先出来的是作者你这篇
等到过完期末再来好好拜读啦
July 20th, 2018
你好,我觉得2式似然函数应该带着积分号,积x比较妥当,或者稍微写一下推导。不然跳跃有点大,因为似然函数应该是是一个求积的形式或者log求和的形式。
你是对的,是我的粗心,已更正。非常感谢。
July 20th, 2018
7式是不是写错了?
July 20th, 2018
5式里VAE的约束是不是应该KL(q||p),而不是KL(p||q)?
$(5),(6),(7)$均没有错。
(7)式里不应该有dz吧,而且VAE的论文中的确是KL(Q||P)啊。
(7)式已经更正,感谢。
为此,我再次去看了一下VAE的论文,并没有发现你说的应该是$KL(Q\Vert P)$的说法。
我一直抓不住你困惑所在的点,所以只好麻烦你留意一下这两点:
1、本文的记号与VAE原论文中的记号不尽相同(比如后验分布我这里是$p(z|x)$,原文是$q(z|x)$);
2、你仿佛从(2),(3)式就开始质疑?(2)式是最大似然,(3)式是等价的KL散度,这点没错吧?(5)式是联合分布的KL散度,你也可以理解为联合的最大似然,这也没错呀。最后的结果也是VAE的标准loss,并不是我独创的新东西。
July 20th, 2018
公式26处所给的例子程序不对号啊。
能否更正一下例子程序的链接?
另外,希望作者写篇关于CVAE-GAN的原理和示例的文章,呵呵。
本文没有开源现成的代码呀,只是表明我所用的代码参考自这个github
https://github.com/LynnHo/DCGAN-LSGAN-WGAN-WGAN-GP-Tensorflow
就在这个的基础上改了两行代码,就不用开源了吧~
文章中对比了实验结果,那加上对比的loss代码也是可以的。麻烦作者辛苦加上吧,呵呵。
应大家要求,已经开放源码~
https://github.com/bojone/gan/tree/master/vgan
July 24th, 2018
读了阁下的文章,感觉对于减少用trick有帮助,大家调自己任务的GAN可以方便点。
前几天还在想实现的问题,今天突然看到你已经公开了。
话说VGAN代码那里的loss部分new regularization并非如文章所说的公式那样的东西,文章公式应该是G0(z)与G1(z)之间的距离,而代码用的是真实图片的距离,反而是一个loss而非penalty的东西。
另外,请问有试过只调lambda的话是否可以不用其他那么多tricks了?
谢谢
感谢指点。
公开的代码就是你说的“G0(z)与G1(z)之间的距离”呀,实现的方法是:在训练完D之后,训练G之前,先用G生成一批$G^o(z)$然后存着备用,然后训练G的之后,就可以代入刚刚的$G^o(z)$,因为$G^o(z)$其实就表现为常数了。此外,所谓penalty,其实也是通过loss实现的,所以这也没有特别明显的界限了,只是觉得它像L2,所以就称为正则项了。
不过,还没测试过详尽地调参。
July 25th, 2018
博主,在GAN的变分推导中,我不明白为什么生成分布q(x|z)=δ(x−G(z))会是个狄拉克函数?最后生成的不是数据吗?
生成器G(z)最后生成的是与x同维度的生成数据,而这个x-G(z)代表样本数据与生成的样本数据的差距,这个差距的结果送入狄拉克函数中代表什么意义呢?
单点分布的意义,可以看成方差无穷小的高斯分布。
July 29th, 2018
博主,你的代码里,似乎跟文章里讲的不大一致吧。代码里每次训练G步应该分了2步,第1步的regularization实际上被抵消了没发生作用,也就是按照传统GAN的方法先更新G网络1步,第2步才是加入regularization后的更新?不知是否理解有误?
$G$的确更新了两步,但两步的性质上是一样的,并没有你说的第一步抵消的说法,因为old_fake我事先算出来了,对于模型来说,它就是常数。在第一步时,正则项为0,但是梯度不为0,因此不能说第一步的正则项没有发挥作用。
原来如此。可是为何不直接用G上一步更新之前的网络,得到的生成样本作为old_fake,这样$G$的训练就没必要每次分2步了。
不是分两步,只是执行两步而已。
也就是说生成器和判别器各自迭代的步数,是人为选定的超参数呀。
可是按照你的做法,两次执行$G$的更新,第一次的regularization里,减去的old_fake并非早一步之前的$G$网络的生成,第二次的old_fake才是$G^o(z)$,这两其实并不一样
前一阶段的$G$的生成样本,就是指当前阶段开始训练$G$之前,用$G$生成的一批样本,不管在公式上还是在代码上,都是这个含义。
所谓当前阶段,就是即将开始训练的阶段;前一阶段,就是已经存在的、在D训练好之前的那个$G$。
说白了,就是希望每次迭代的时候,$G(z)$的改变量不要太大,所以先生成一批旧的样本(已经sess.run),然后加上L2。
还是不太明白。
代码里,两次G更新用的old_fake是相同的,对于第二次更新来说,old_fake确实是早一步G参数下算出来的生成数据,但是对于第一次,它不就是当前状态下生成的吗?除非对于$G^o(z)$的定义在两次更新下是不同的,否则的话,要么在第一次更新执行后重新生成一次old_fake,要么在上一个迭代步里保存一个G更新之前的生成作为下一步用到的$G^o(z)$,否则的话两者就是不对等的啊
我觉得zero说的有道理,你的做法是G执行两次,第一次产生G0(此时正则项=0,但是更新了G)然后第二次产生了G1,此时更新G(正则项不等于0)。既然这样,假如我训练时候保存上一次训练的G产生的old_fake,没必要G执行两次,在本次是z_ipt随机产生,和上次的old_fake产生正则项(此时不等于0)更新G呢?
要保证z相同
July 30th, 2018
@zoro|comment-9536
1、当前时刻$G$训练完毕,那么它就成为了$G^o$;
2、然后轮到$D$训练,将$D$训练到最优,那么就得到理论解$(18)$;
3、现在又轮到训练$G$了,训练之前先用$G$生成一批样本,注意这时候$G$还没有改变,所以生成的样本就是$G^o(z)$,保存下来,作为正则项$\Vert G(z) - G^o(z)\Vert^2$加入到$G$的训练中。不管迭代多少步都是这样写,每一步都没有本质差别。但是,由于正则项是二次型的,所以只有第二步开始,正则项才生效。
August 15th, 2018
苏老师,你好,在博文的叙述中,我有些小问题想请教:
在VAE的推导中,有一段话:“因为$q(x|z),p(z|x)$为带有神经网络的高斯分布”,我觉得有问题。p(z|x)是高斯分布没错,这时编码器决定的条件分布,而$q(x|z)$则不应该是高斯分布了,$q(x|z)$是$q(z)$经过Decoder映射的结果,q(z)是高斯分布,若两者都是高斯分布,则$q(x,z)=q(x|z)q(z)$就是高斯分布了,不符合拟合的要求。另外,在整个VAE的过程中并没有对q(x|z)的类型进行约束,不应该下此结论。
不知对不对,还请苏老师指正。
1. $q(x|z)$的确是高斯分布,因为一般情况下,我们采用mse作为重构损失,而重构损失对应的是$-\log q(x|z)$这一项,所以
$$-\log q(x|z)\sim (x-G(z))^2$$
也就是$q(x|z)\sim e^{-(x-G(z))^2}$,这就是关于$x$的高斯分布。
2.$q(x|z),q(z)$都是高斯分布,也不能说明$q(x,z)=q(x|z)q(z)$是高斯分布。
3. $q(x|z)$是高斯分布,只是一个近似假设,不得已而为之。
苏老师,您好。感谢您百忙之中回我的问题,但我仍在此有些不解:
1、两个高斯分布相乘,就是高斯分布,这可以从公式中推导出来。
2、在推导VAE时,并不需要限制$q(x \vert z)$必须是高斯分布,推导过程如下:
在VAE中,可令$q(\mathbf z)$为标准正态分布,$p(\mathbf z \vert \mathbf x)$为正态分布,而$q(\mathbf x \vert \mathbf z)$为随机变量$\mathbf z$ 到空间 $\mathbf X$的映射的随机分布的密度。回到联合概率分布KL散度:
$$
KL(p(\mathbf x, \mathbf z)\Vert q(\mathbf x, \mathbf z))=\iint p(\mathbf x, \mathbf z) \log \frac {p(\mathbf x, \mathbf z)}{q(\mathbf x, \mathbf z)} d\mathbf x d\mathbf z \\ =\iint p(\mathbf z \vert \mathbf x)p(\mathbf x) \log \frac {p(\mathbf z \vert \mathbf x)p(\mathbf x)}{q(\mathbf x \vert \mathbf z)q(\mathbf z)}d\mathbf x d\mathbf z \\ = \iint p(\mathbf z \vert \mathbf x)p(\mathbf x) \ [\log p(\mathbf z \vert \mathbf x) + \log p(\mathbf x) - \log q(\mathbf x \vert \mathbf z) - \log q(\mathbf z)] d\mathbf x d\mathbf z \\ =\iint p(\mathbf z \vert \mathbf x)p(\mathbf x) \log p(\mathbf x)d\mathbf x d\mathbf z - \iint p(\mathbf z \vert \mathbf x)p(\mathbf x) \log q(\mathbf x \vert \mathbf z)d\mathbf x d\mathbf z + \iint p(\mathbf z \vert \mathbf x)p(\mathbf x)\log \frac {p(\mathbf z \vert \mathbf x)}{q(\mathbf z)} d\mathbf x d\mathbf z \qquad(1)
$$
1、右边第一项是$\iint p(\mathbf x,\mathbf z )p(\mathbf x) \log p(\mathbf x)d\mathbf x d\mathbf z$ 是真实分布的积分,与VAE可调参数无关,因而在优化时无需考虑,可忽略。
2、第三项有:
$$
\iint p(\mathbf z \vert \mathbf x)p(\mathbf x)\log \frac {p(\mathbf z \vert \mathbf x)}{q(\mathbf z)} d\mathbf x d\mathbf z = \mathbf E_{\mathbf x \sim p(\mathbf x)}\left(\int p(\mathbf z \vert \mathbf x)\log \frac {p(\mathbf z \vert \mathbf x)}{q(\mathbf z)} d\mathbf z \right) \\ = \mathbf E_{\mathbf x \sim p(\mathbf x)}(KL(p(\mathbf z \vert \mathbf x) \Vert q(\mathbf z))) \qquad(2)
$$
3、第二项有:
$$
\iint p(\mathbf z \vert \mathbf x)p(\mathbf x) \log q(\mathbf x \vert \mathbf z)d\mathbf x d\mathbf z = \int p(\mathbf x)\int p(\mathbf z \vert \mathbf x) \log q(\mathbf x \vert \mathbf z)d\mathbf x d\mathbf z = \mathbf E_{\mathbf x\sim p(\mathbf x)}\left(\int p(\mathbf z \vert \mathbf x) \log q(\mathbf x \vert \mathbf z)d\mathbf z\right) \qquad(3)
$$
若 $\mathbf x\sim p(\mathbf x)$ 仅抽样1个点,得到 $\mathbf x_i$ 作为Encoder的输入,求$\mathbf x\sim p(\mathbf x)$的期望就失去了意义,则(4)式变形为:
$$
\iint p(\mathbf z \vert \mathbf x)p(\mathbf x) \log q(\mathbf x \vert \mathbf z)d\mathbf x d\mathbf z = \int p(\mathbf z \vert \mathbf x_i) \log q(\mathbf x \vert \mathbf z)d\mathbf z \\ = \mathbf E_{\mathbf z\sim p(\mathbf z \vert \mathbf x_i)}\left( \log q(\mathbf x \vert \mathbf z) \right) \qquad(4)
$$
最后,VAE的Loss变为:
$$
KL(p(\mathbf x, \mathbf z)\Vert q(\mathbf x, \mathbf z)) \sim -\log q(\mathbf x_i \vert \mathbf z_i) \ + \ \mathbf E_{\mathbf x \sim p(\mathbf x)}(KL(p(\mathbf z \vert \mathbf x) \Vert q(\mathbf z))) \qquad(5)
$$
与原推导结果一致。
3、$q(x \vert z)$反映的是Decoder对z的映射,此映射将正态分布之z映射到其他的空间上,形成新的概率分布,并不要求是高斯分布,而且也不应该是高斯分布。
1、$q(x|z)$是高斯分布,但它的均值$\mu$是$z$的复杂函数$G(z)$,所以$q(x|z)q(z)$的指数部分关于$z$并不是二次的,所以它不是高斯分布。
2、你后面的推导都没有错呀,$(5)$式也没有错,推导过程确实不需要$q(x|z)$是高斯分布的假设。但是接下来呢?你是不是得代入计算呀?你代入的$q(x|z)$是什么呢?如果你用mse做重构误差,那不就是$-\log q(x|z)=\Vert x-G(z)\Vert^2$了吗?这就说明$q(x|z)$是高斯分布呀,这一点在VAE的原始论文就说明了。如果是二值输出,也可以用二值交叉熵,这时候对应的$q(x|z)$是伯努利分布。不同的loss确实对应不同的分布,但最常见的是mse确实对应了高斯分布。
3、真实的$q(x|z)$的确不是高斯分布,但是VAE的目的是用一个高斯分布(或者其他能写出的分布)去近似真实的$q(x|z)$。为什么是高斯?因为高斯好算呀...
多谢苏老师,我重看了原文,确实如此,多谢多谢!希望以后还能多多跟您学习!