变分自编码器（一）：原来是这么一回事

过去虽然没有细看，但印象里一直觉得变分自编码器（Variational Auto-Encoder，VAE）是个好东西。于是趁着最近看概率图模型的三分钟热度，我决定也争取把VAE搞懂。于是乎照样翻了网上很多资料，无一例外发现都很含糊，主要的感觉是公式写了一大通，还是迷迷糊糊的，最后好不容易觉得看懂了，再去看看实现的代码，又感觉实现代码跟理论完全不是一回事啊。

终于，东拼西凑再加上我这段时间对概率模型的一些积累，并反复对比原论文《Auto-Encoding Variational Bayes》，最后我觉得我应该是想明白了。其实真正的VAE，跟很多教程说的的还真不大一样，很多教程写了一大通，都没有把模型的要点写出来～于是写了这篇东西，希望通过下面的文字，能把VAE初步讲清楚。

分布变换 #

通常我们会拿VAE跟GAN比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量$Z$生成目标数据$X$的模型，但是实现上有所不同。更准确地讲，它们是假设了$Z$服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型$X=g(Z)$，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

那现在假设$Z$服从标准的正态分布，那么我就可以从中采样得到若干个$Z_1, Z_2, \dots, Z_n$，然后对它做变换得到$\hat{X}_1 = g(Z_1),\hat{X}_2 = g(Z_2),\dots,\hat{X}_n = g(Z_n)$，我们怎么判断这个通过$g$构造出来的数据集，它的分布跟我们目标的数据集分布是不是一样的呢？有读者说不是有KL散度吗？当然不行，因为KL散度是根据两个概率分布的表达式来算它们的相似度的，然而目前我们并不知道它们的概率分布的表达式，我们只有一批从构造的分布采样而来的数据$\{\hat{X}_1,\hat{X}_2,\dots,\hat{X}_n\}$，还有一批从真实的分布采样而来的数据$\{X_1,X_2,\dots,X_n\}$（也就是我们希望生成的训练集）。我们只有样本本身，没有分布表达式，当然也就没有方法算KL散度。

虽然遇到困难，但还是要想办法解决的。GAN的思路很直接粗犷：既然没有合适的度量，那我干脆把这个度量也用神经网络训练出来吧。就这样，WGAN就诞生了，详细过程请参考《互怼的艺术：从零直达WGAN-GP》。而VAE则使用了一个精致迂回的技巧。

VAE慢谈 #

这一部分我们先回顾一般教程是怎么介绍VAE的，然后再探究有什么问题，接着就自然地发现了VAE真正的面目。

经典回顾 #

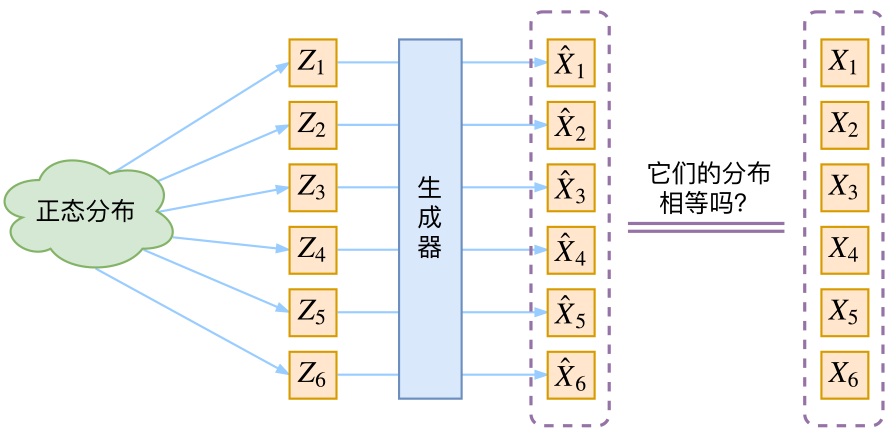
首先我们有一批数据样本$\{X_1,\dots,X_n\}$，其整体用$X$来描述，我们本想根据$\{X_1,\dots,X_n\}$得到$X$的分布$p(X)$，如果能得到的话，那我直接根据$p(X)$来采样，就可以得到所有可能的$X$了（包括$\{X_1,\dots,X_n\}$以外的），这是一个终极理想的生成模型了。当然，这个理想很难实现，于是我们将分布改一改
$$p(X)=\sum_Z p(X|Z)p(Z)\tag{1}$$
这里我们就不区分求和还是求积分了，意思对了就行。此时$p(X|Z)$就描述了一个由$Z$来生成$X$的模型，而我们假设$Z$服从标准正态分布，也就是$p(Z)=\mathcal{N}(0,I)$。如果这个理想能实现，那么我们就可以先从标准正态分布中采样一个$Z$，然后根据$Z$来算一个$X$，也是一个很棒的生成模型。接下来就是结合自编码器来实现重构，保证有效信息没有丢失，再加上一系列的推导，最后把模型实现。框架的示意图如下：

看出了什么问题了吗？如果像这个图的话，我们其实完全不清楚：究竟经过重新采样出来的$Z_k$，是不是还对应着原来的$X_k$，所以我们如果直接最小化$\mathcal{D}(\hat{X}_k,X_k)^2$（这里$\mathcal{D}$代表某种距离函数）是很不科学的，而事实上你看代码也会发现根本不是这样实现的。也就是说，很多教程说了一大通头头是道的话，然后写代码时却不是按照所写的文字来写，可是他们也不觉得这样会有矛盾～

VAE初现 #

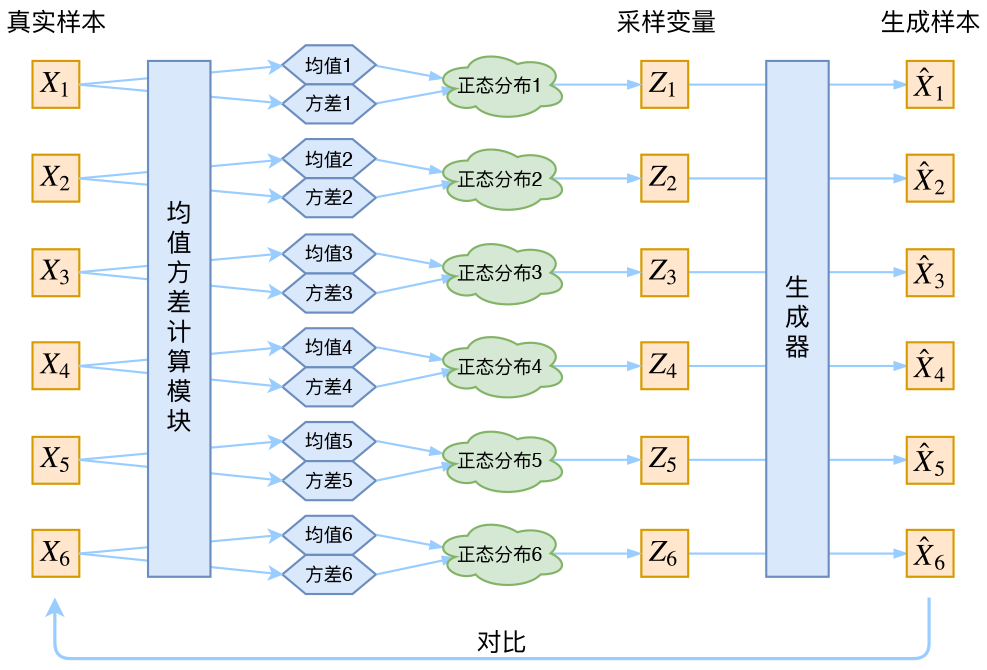
其实，在整个VAE模型中，我们并没有去使用$p(Z)$（隐变量空间的分布）是正态分布的假设，我们用的是假设$p(Z|X)$（后验分布）是正态分布！！

具体来说，给定一个真实样本$X_k$，我们假设存在一个专属于$X_k$的分布$p(Z|X_k)$（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布。为什么要强调“专属”呢？因为我们后面要训练一个生成器$X=g(Z)$，希望能够把从分布$p(Z|X_k)$采样出来的一个$Z_k$还原为$X_k$。如果假设$p(Z)$是正态分布，然后从$p(Z)$中采样一个$Z$，那么我们怎么知道这个$Z$对应于哪个真实的$X$呢？现在$p(Z|X_k)$专属于$X_k$，我们有理由说从这个分布采样出来的$Z$应该要还原到$X_k$中去。

事实上，在论文《Auto-Encoding Variational Bayes》的应用部分，也特别强调了这一点：

In this case, we can let the
variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure:
$$\log q_{\phi}(\boldsymbol{z}|\boldsymbol{x}^{(i)}) = \log \mathcal{N}(\boldsymbol{z} ;\boldsymbol{\mu}^{(i)},\boldsymbol{\sigma}^{2(i)}\boldsymbol{I})\tag{9}$$

（注：这里是直接摘录原论文，本文所用的符号跟原论文不尽一致，望读者不会混淆。）

论文中的式$(9)$是实现整个模型的关键，不知道为什么很多教程在介绍VAE时都没有把它凸显出来。尽管论文也提到$p(Z)$是标准正态分布，然而那其实并不是本质重要的。

回到本文，这时候每一个$X_k$都配上了一个专属的正态分布，才方便后面的生成器做还原。但这样有多少个$X$就有多少个正态分布了。我们知道正态分布有两组参数：均值$\mu$和方差$\sigma^2$（多元的话，它们都是向量），那我怎么找出专属于$X_k$的正态分布$p(Z|X_k)$的均值和方差呢？好像并没有什么直接的思路。那好吧，那我就用神经网络来拟合出来吧！这就是神经网络时代的哲学：难算的我们都用神经网络来拟合，在WGAN那里我们已经体验过一次了，现在再次体验到了。

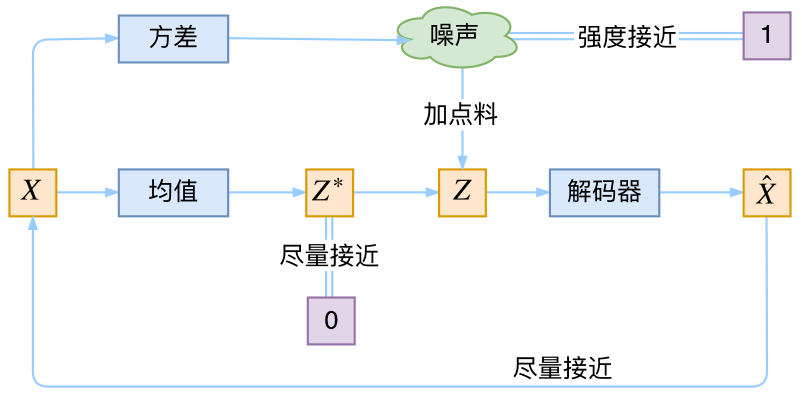
于是我们构建两个神经网络$\mu_k = f_1(X_k),\log \sigma_k^2 = f_2(X_k)$来算它们了。我们选择拟合$\log \sigma_k^2$而不是直接拟合$\sigma_k^2$，是因为$\sigma_k^2$总是非负的，需要加激活函数处理，而拟合$\log \sigma_k^2$不需要加激活函数，因为它可正可负。到这里，我能知道专属于$X_k$的均值和方差了，也就知道它的正态分布长什么样了，然后从这个专属分布中采样一个$Z_k$出来，然后经过一个生成器得到$\hat{X}_k=g(Z_k)$，现在我们可以放心地最小化$\mathcal{D}(\hat{X}_k,X_k)^2$，因为$Z_k$是从专属$X_k$的分布中采样出来的，这个生成器应该要把开始的$X_k$还原回来。于是可以画出VAE的示意图

分布标准化 #

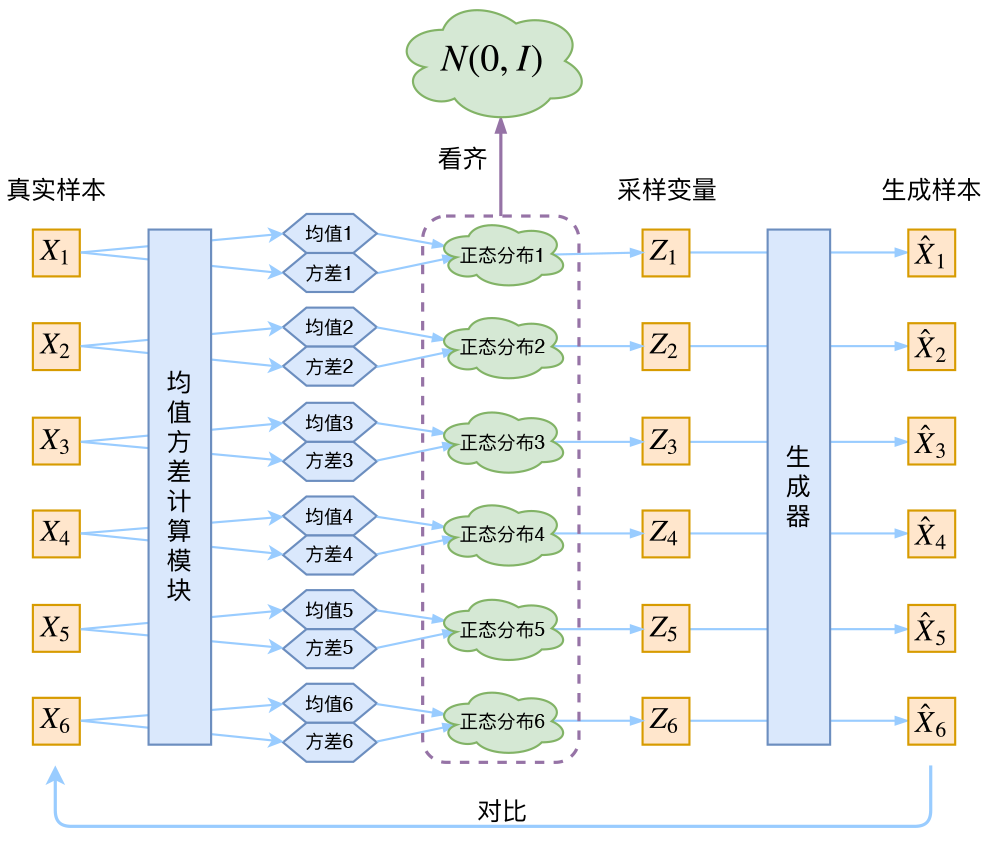
让我们来思考一下，根据上图的训练过程，最终会得到什么结果。

首先，我们希望重构$X$，也就是最小化$\mathcal{D}(\hat{X}_k,X_k)^2$，但是这个重构过程受到噪声的影响，因为$Z_k$是通过重新采样过的，不是直接由encoder算出来的。显然噪声会增加重构的难度，不过好在这个噪声强度（也就是方差）通过一个神经网络算出来的，所以最终模型为了重构得更好，肯定会想尽办法让方差为0。而方差为0的话，也就没有随机性了，所以不管怎么采样其实都只是得到确定的结果（也就是均值），只拟合一个当然比拟合多个要容易，而均值是通过另外一个神经网络算出来的。

说白了，模型会慢慢退化成普通的AutoEncoder，噪声不再起作用。

这样不就白费力气了吗？说好的生成模型呢？

别急别急，其实VAE还让所有的$p(Z|X)$都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。怎么理解“保证了生成能力”呢？如果所有的$p(Z|X)$都很接近标准正态分布$\mathcal{N}(0,I)$，那么根据定义
$$p(Z)=\sum_X p(Z|X)p(X)=\sum_X \mathcal{N}(0,I)p(X)=\mathcal{N}(0,I) \sum_X p(X) = \mathcal{N}(0,I)\tag{2}$$
这样我们就能达到我们的先验假设：$p(Z)$是标准正态分布。然后我们就可以放心地从$\mathcal{N}(0,I)$中采样来生成图像了。

那怎么让所有的$p(Z|X)$都向$\mathcal{N}(0,I)$看齐呢？如果没有外部知识的话，其实最直接的方法应该是在重构误差的基础上中加入额外的loss：
$$\mathcal{L}_{\mu}=\Vert f_1(X_k)\Vert^2\quad \text{和}\quad \mathcal{L}_{\sigma^2}=\Vert f_2(X_k)\Vert^2\tag{3}$$
因为它们分别代表了均值$\mu_k$和方差的对数$\log\sigma_k^2$，达到$\mathcal{N}(0,I)$就是希望二者尽量接近于0了。不过，这又会面临着这两个损失的比例要怎么选取的问题，选取得不好，生成的图像会比较模糊。所以，原论文直接算了一般（各分量独立的）正态分布与标准正态分布的KL散度$KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,I)\Big)$作为这个额外的loss，计算结果为
$$\mathcal{L}_{\mu,\sigma^2}=\frac{1}{2} \sum_{i=1}^d \Big(\mu_{(i)}^2 + \sigma_{(i)}^2 - \log \sigma_{(i)}^2 - 1\Big)\tag{4}$$
这里的$d$是隐变量$Z$的维度，而$\mu_{(i)}$和$\sigma_{(i)}^2$分别代表一般正态分布的均值向量和方差向量的第$i$个分量。直接用这个式子做补充loss，就不用考虑均值损失和方差损失的相对比例问题了。显然，这个loss也可以分两部分理解：
$$\begin{aligned}&\mathcal{L}_{\mu,\sigma^2}=\mathcal{L}_{\mu} + \mathcal{L}_{\sigma^2}\\
&\mathcal{L}_{\mu}=\frac{1}{2} \sum_{i=1}^d \mu_{(i)}^2=\frac{1}{2}\Vert f_1(X)\Vert^2\\
&\mathcal{L}_{\sigma^2}=\frac{1}{2} \sum_{i=1}^d\Big(\sigma_{(i)}^2 - \log \sigma_{(i)}^2 - 1\Big)\end{aligned}\tag{5}$$

推导
由于我们考虑的是各分量独立的多元正态分布，因此只需要推导一元正态分布的情形即可，根据定义我们可以写出
$$\begin{aligned}&KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,1)\Big)\\
=&\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \left(\log \frac{e^{-(x-\mu)^2/2\sigma^2}/\sqrt{2\pi\sigma^2}}{e^{-x^2/2}/\sqrt{2\pi}}\right)dx\\
=&\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \log \left\{\frac{1}{\sqrt{\sigma^2}}\exp\left\{\frac{1}{2}\big[x^2-(x-\mu)^2/\sigma^2\big]\right\} \right\}dx\\
=&\frac{1}{2}\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \Big[-\log \sigma^2+x^2-(x-\mu)^2/\sigma^2 \Big] dx\end{aligned}$$

整个结果分为三项积分，第一项实际上就是$-\log \sigma^2$乘以概率密度的积分（也就是1），所以结果是$-\log \sigma^2$；第二项实际是正态分布的二阶矩，熟悉正态分布的朋友应该都清楚正态分布的二阶矩为$\mu^2+\sigma^2$；而根据定义，第三项实际上就是“-方差除以方差=-1”。所以总结果就是$$KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,1)\Big)=\frac{1}{2}\Big(-\log \sigma^2+\mu^2+\sigma^2-1\Big)$$

重参数技巧 #

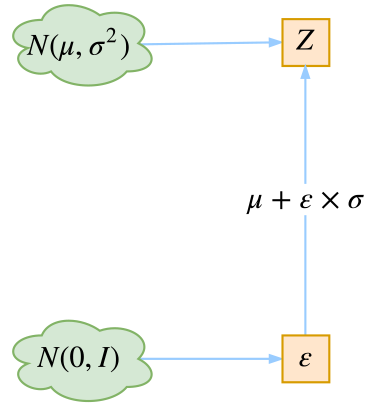
最后是实现模型的一个技巧，英文名是reparameterization trick，我这里叫它做重参数吧。其实很简单，就是我们要从$p(Z|X_k)$中采样一个$Z_k$出来，尽管我们知道了$p(Z|X_k)$是正态分布，但是均值方差都是靠模型算出来的，我们要靠这个过程反过来优化均值方差的模型，但是“采样”这个操作是不可导的，而采样的结果是可导的。我们利用
$$\begin{aligned}&\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(z-\mu)^2}{2\sigma^2}\right)dz \\
=& \frac{1}{\sqrt{2\pi}}\exp\left[-\frac{1}{2}\left(\frac{z-\mu}{\sigma}\right)^2\right]d\left(\frac{z-\mu}{\sigma}\right)\end{aligned}\tag{6}$$
这说明$(z-\mu)/\sigma=\varepsilon$是服从均值为0、方差为1的标准正态分布的，要同时把$dz$考虑进去，是因为乘上$dz$才算是概率，去掉$dz$是概率密度而不是概率。这时候我们得到：

从$\mathcal{N}(\mu,\sigma^2)$中采样一个$Z$，相当于从$\mathcal{N}(0,I)$中采样一个$\varepsilon$，然后让$Z=\mu + \varepsilon \times \sigma$。

于是，我们将从$\mathcal{N}(\mu,\sigma^2)$采样变成了从$\mathcal{N}(0,I)$中采样，然后通过参数变换得到从$\mathcal{N}(\mu,\sigma^2)$中采样的结果。这样一来，“采样”这个操作就不用参与梯度下降了，改为采样的结果参与，使得整个模型可训练了。

具体怎么实现，大家把上述文字对照着代码看一下，一下子就明白了～

后续分析 #

即便把上面的所有内容都搞清楚了，面对VAE，我们可能还存有很多疑问。

本质是什么 #

VAE的本质是什么？VAE虽然也称是AE（AutoEncoder）的一种，但它的做法（或者说它对网络的诠释）是别具一格的。在VAE中，它的Encoder有两个，一个用来计算均值，一个用来计算方差，这已经让人意外了：Encoder不是用来Encode的，是用来算均值和方差的，这真是大新闻了，还有均值和方差不都是统计量吗，怎么是用神经网络来算的？

事实上，我觉得VAE从让普通人望而生畏的变分和贝叶斯理论出发，最后落地到一个具体的模型中，虽然走了比较长的一段路，但最终的模型其实是很接地气的：它本质上就是在我们常规的自编码器的基础上，对encoder的结果（在VAE中对应着计算均值的网络）加上了“高斯噪声”，使得结果decoder能够对噪声有鲁棒性；而那个额外的KL loss（目的是让均值为0，方差为1），事实上就是相当于对encoder的一个正则项，希望encoder出来的东西均有零均值。

那另外一个encoder（对应着计算方差的网络）的作用呢？它是用来动态调节噪声的强度的。直觉上来想，当decoder还没有训练好时（重构误差远大于KL loss），就会适当降低噪声（KL loss增加），使得拟合起来容易一些（重构误差开始下降）；反之，如果decoder训练得还不错时（重构误差小于KL loss），这时候噪声就会增加（KL loss减少），使得拟合更加困难了（重构误差又开始增加），这时候decoder就要想办法提高它的生成能力了。

说白了，重构的过程是希望没噪声的，而KL loss则希望有高斯噪声的，两者是对立的。所以，VAE跟GAN一样，内部其实是包含了一个对抗的过程，只不过它们两者是混合起来，共同进化的。从这个角度看，VAE的思想似乎还高明一些，因为在GAN中，造假者在进化时，鉴别者是安然不动的，反之亦然。当然，这只是一个侧面，不能说明VAE就比GAN好。GAN真正高明的地方是：它连度量都直接训练出来了，而且这个度量往往比我们人工想的要好（然而GAN本身也有各种问题，这就不展开了）。

从这个讨论中，我们也可以看出，当然，每个$p(Z|X)$是不可能完全精确等于标准正态分布，否则$p(Z|X)$就相当于跟$X$无关了，重构效果将会极差。最终的结果就会是，$p(Z|X)$保留了一定的$X$信息，重构效果也还可以，并且$(2)$近似成立，所以同时保留着生成能力。

正态分布？ #

对于$p(Z|X)$的分布，读者可能会有疑惑：是不是必须选择正态分布？可以选择均匀分布吗？

估计不大可行，这还是因为KL散度的计算公式：
$$KL\Big(p(x)\Big\Vert q(x)\Big) = \int p(x) \ln \frac{p(x)}{q(x)}dx\tag{7}$$
要是在某个区域中$p(x)\neq 0$而$q(x)=0$的话，那么KL散度就无穷大了。对于正态分布来说，所有点的概率密度都是非负的，因此不存在这个问题。但对于均匀分布来说，只要两个分布不一致，那么就必然存在$p(x)\neq 0$而$q(x)=0$的区间，因此KL散度会无穷大。当然，写代码时我们会防止这种除零错误，但依然避免不了KL loss占比很大，因此模型会迅速降低KL loss，也就是后验分布$p(Z|X)$迅速趋于先验分布$p(Z)$，而噪声和重构无法起到对抗作用。这又回到我们开始说的，无法区分哪个$z$对应哪个$x$了。

当然，非得要用均匀分布也不是不可能，就是算好两个均匀分布的KL散度，然后做好除零错误处理，加大重构loss的权重，等等～但这样就显得太丑陋了。

变分在哪里 #

还有一个有意思（但不大重要）的问题是：VAE叫做“变分自编码器”，它跟变分法有什么联系？在VAE的论文和相关解读中，好像也没看到变分法的存在呀？

呃～其实如果读者已经承认了KL散度的话，那VAE好像真的跟变分没多大关系了～因为理论上对于KL散度$(7)$我们要证明：

固定概率分布$p(x)$（或$q(x)$）的情况下，对于任意的概率分布$q(x)$（或$p(x)$），都有$KL\Big(p(x)\Big\Vert q(x)\Big)\geq 0$，而且只有当$p(x)=q(x)$时才等于零。

因为$KL\Big(p(x)\Big\Vert q(x)\Big)$实际上是一个泛函，要对泛函求极值就要用到变分法，当然，这里的变分法只是普通微积分的平行推广，还没涉及到真正复杂的变分法。而VAE的变分下界，是直接基于KL散度就得到的。所以直接承认了KL散度的话，就没有变分的什么事了。

一句话，VAE的名字中“变分”，是因为它的推导过程用到了KL散度及其性质。

条件VAE #

最后，因为目前的VAE是无监督训练的，因此很自然想到：如果有标签数据，那么能不能把标签信息加进去辅助生成样本呢？这个问题的意图，往往是希望能够实现控制某个变量来实现生成某一类图像。当然，这是肯定可以的，我们把这种情况叫做Conditional VAE，或者叫CVAE。（相应地，在GAN中我们也有个CGAN。）

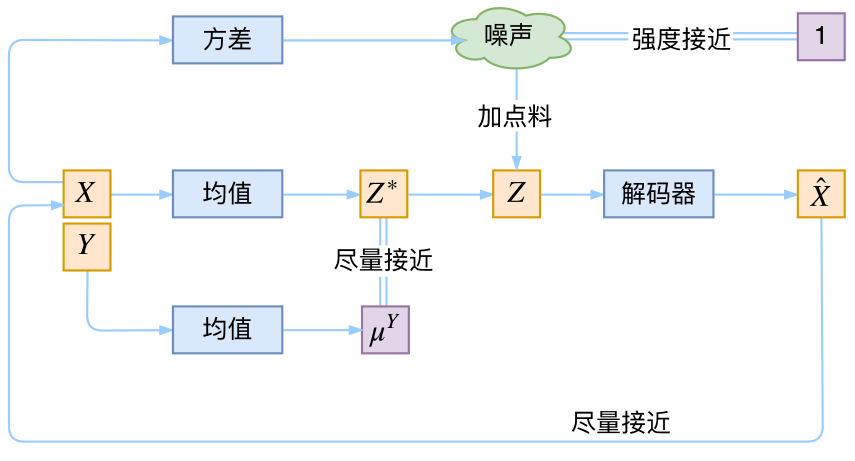
但是，CVAE不是一个特定的模型，而是一类模型，总之就是把标签信息融入到VAE中的方式有很多，目的也不一样。这里基于前面的讨论，给出一种非常简单的VAE。

在前面的讨论中，我们希望$X$经过编码后，$Z$的分布都具有零均值和单位方差，这个“希望”是通过加入了KL loss来实现的。如果现在多了类别信息$Y$，我们可以希望同一个类的样本都有一个专属的均值$\mu^Y$（方差不变，还是单位方差），这个$\mu^Y$让模型自己训练出来。这样的话，有多少个类就有多少个正态分布，而在生成的时候，我们就可以通过控制均值来控制生成图像的类别。事实上，这样可能也是在VAE的基础上加入最少的代码来实现CVAE的方案了，因为这个“新希望”也只需通过修改KL loss实现：
$$\mathcal{L}_{\mu,\sigma^2}=\frac{1}{2} \sum_{i=1}^d\Big[\big(\mu_{(i)}-\mu^Y_{(i)}\big)^2 + \sigma_{(i)}^2 - \log \sigma_{(i)}^2 - 1\Big]\tag{8}$$
下图显示这个简单的CVAE是有一定的效果的，不过因为encoder和decoder都比较简单（纯MLP），所以控制生成的效果不尽完美。更完备的CVAE请读者自行学习了，最近还出来了CVAE与GAN结合的工作CVAE-GAN，模型套路千变万化啊。

代码 #

我把Keras官方的VAE代码复制了一份，然后微调并根据前文内容添加了中文注释，也把最后说到的简单的CVAE实现了一下，供读者参考～

代码：https://github.com/bojone/vae

终点站 #

磕磕碰碰，又到了文章的终点了。不知道讲清楚了没，希望大家多提点意见～

总的来说，VAE的思路还是很漂亮的。倒不是说它提供了一个多么好的生成模型（因为事实上它生成的图像并不算好，偏模糊），而是它提供了一个将概率图跟深度学习结合起来的一个非常棒的案例，这个案例有诸多值得思考回味的地方。

转载到请包括本文地址：https://kexue.fm/archives/5253

更详细的转载事宜请参考：《科学空间FAQ》