三味Capsule:矩阵Capsule与EM路由
By 苏剑林 | 2018-03-02 | 269728位读者 |事实上,在论文《Dynamic Routing Between Capsules》发布不久后,一篇新的Capsule论文《Matrix Capsules with EM Routing》就已经匿名公开了(在ICLR 2018的匿名评审中),而如今作者已经公开,他们是Geoffrey Hinton, Sara Sabour, Nicholas Frosst。不出大家意料,作者果然有Hinton。
大家都知道,像Hinton这些“鼻祖级”的人物,发表出来的结果一般都是比较“重磅”的。那么,这篇新论文有什么特色呢?
在笔者的思考过程中,文章《Understanding Matrix capsules with EM Routing 》给了我颇多启示,知乎上各位大神的相关讨论也加速了我的阅读,在此表示感谢。
论文摘要 #
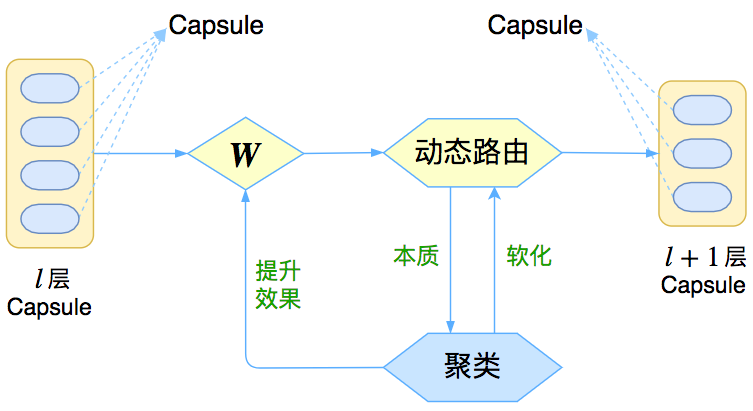
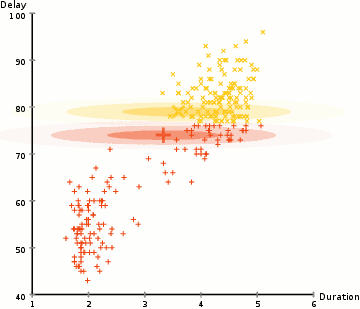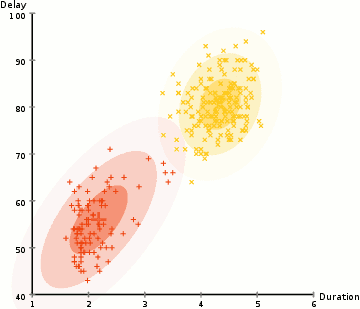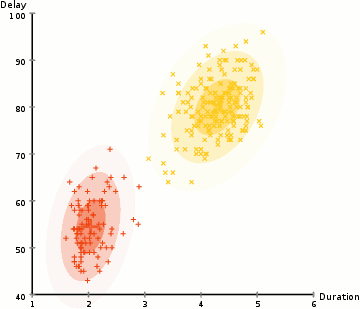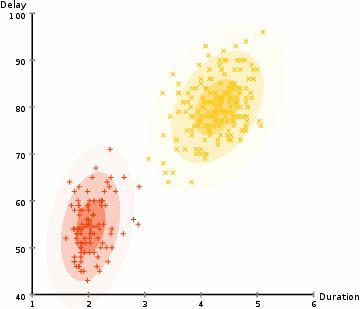
让我们先来回忆一下上一篇介绍《再来一顿贺岁宴:从K-Means到Capsule》中的那个图
这个图表明,Capsule事实上描述了一个建模的框架,这个框架中的东西很多都是可以自定义的,最明显的是聚类算法,可以说“有多少种聚类算法就有多少种动态路由”。那么这次Hinton修改了什么呢?总的来说,这篇新论文有以下几点新东西:
1、原来用向量来表示一个Capsule,现在用矩阵来表示;
2、聚类算法换成了GMM(高斯混合模型);
3、在实验部分,实现了Capsule版的卷积。
一波疑问 #
事实上,看到笔者提出的这三点新东西,读者应该就会有很多想法和疑问了,比如:
向量 vs 矩阵 #
矩阵和向量有什么区别呢?矩阵不也可以展平为向量吗?
其实是有点区别的。比如一个$4\times 4$的矩阵,跟一个16维的向量,有什么差别呢?答案是矩阵的不同位置的元素重要性不一样,而向量的每个元素的重要性都是一样的。熟悉线性代数的读者应该也可以感觉到,一个矩阵的对角线元素的地位“看起来”是比其他元素要重要一些的。从计算的角度看,也能发现区别:要将一个16维的向量变换为另外一个16维的向量,我们需要一个$16\times 16$的变换矩阵;但如果将一个$4\times 4$的矩阵变换为另外一个$4\times 4$的矩阵,那么只需要一个$4\times 4$的变换矩阵,参数量减少了。从这个角度看,也许将Capsule从向量变为矩阵的根本目的是降低计算量。
立方阵? #
以后的Capsule可能是“立方阵”甚至更高阶张量吗?
不大可能。因为更高阶张量的乘法本质上也是二阶矩阵的乘法。
GMM vs K-Means #
GMM聚类与你之前说的K-Means聚类差别大吗?
这个得从两个角度看。一方面,GMM可以看成是K-Means的升级版,而且它本身就是可导的,不需要之前的“软化”技巧,如果在K-Means中使用欧氏距离的话,那么K-Means就是GMM的一个极限版本;但另一方面,K-Means允许我们更灵活地使用其他相似的度量,而GMM中相当于只能用(加权的)欧氏距离,也就是把度量“写死”了,这算是个缺点。总的来说,两者半斤八两吧。
Capsule版的卷积 #
Capsule版的卷积是怎么回事?为什么前一篇论文没有呢?
我们所说的动态路由,事实上就只相当于深度学习中的全连接层,而深度学习中的卷积层则是局部的全连接层。那么很显然,只需要弄个“局部动态路由”,那么就得到了Capsule版的卷积了。这个东西事实上在Hinton上一篇论文就应该出现,因为它跟具体的路由算法并没有关系,但不知为何,Hinton在这篇新论文才实现了它。
GMM模型简介 #
既然这篇新论文用到了GMM来聚类,那么就要花点功夫来学习一下GMM了。理解GMM算法是一件非常有意思的事情,哪怕不是因为Capsule——因为GMM模型能够大大加深我们对概率模型和机器学习理论(尤其是无监督学习理论)的理解。预告一下,在下面的内容中,笔者还较大地简化了GMM的推导过程,相信能降低读者的理解难度。
当然,只想理解Capsule核心思想的读者,可以有选择地跳过比较理论化的部分。
本质 #
事实上,在我们脑海里最好不要将GMM视为一个聚类算法,而将它看作一个真正的无监督学习算法,它试图学习数据的分布。数据本身是个体,而分布则是一个整体,从研究数据本身到研究数据分布,是质的改变。
GMM,全称Gaussian Mixed Model,即高斯混合模型;当然学界还有另一个GMM——Generalized Method of Moments ,是用来估计参数的广义矩估计方法,但这里讨论的是前者。具体来说,对于已有的向量$\boldsymbol{x}_1,\dots,\boldsymbol{x}_n$,GMM希望找到它们所满足的分布$p(\boldsymbol{x})$。当然,不能漫无目的地找,得整一个比较简单的形式出来。GMM设想这批数据能分为几部分(类别),每部分单独研究,也就是
$$p(\boldsymbol{x})=\sum\limits_{j=1}^k p(j)p(\boldsymbol{x}|j)\tag{1}$$
其中$j$代表了类别,取值为$1,2,\dots,k$,由于$p(j)$跟$\boldsymbol{x}$没关系,因此可以认为它是个常数分布,记$p(j)=\pi_j$。然后$p(\boldsymbol{x}|j)$就是这个类内的概率分布,GMM的特性就是用概率分布来描述一个类。那么它取什么好呢?我们取最简单的正态分布,注意这里$\boldsymbol{x}$是个向量,因此我们要考虑多元的正态分布,一般形式为
$$N(\boldsymbol{x};\boldsymbol{\mu}_j,\boldsymbol{\Sigma}_j)=\frac{1}{(2\pi)^{d/2}(\det\boldsymbol{\Sigma}_j)^{1/2}}\exp\left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu}_j)^{\top}\boldsymbol{\Sigma}_j^{-1}(\boldsymbol{x}-\boldsymbol{\mu}_j)\right)\tag{2}$$
其中$d$是向量$\boldsymbol{x}$的分量个数。现在我们得到模型的基本形式
$$\begin{aligned}p(\boldsymbol{x})=\sum\limits_{j=1}^k p(&j)\times p(\boldsymbol{x}|j)=\sum\limits_{j=1}^k\pi_j N(\boldsymbol{x};\boldsymbol{\mu}_j,\boldsymbol{\Sigma}_j)\\
\downarrow& \qquad\,\,\downarrow\\
\pi_j& \,\,\cdot\,\, N(\boldsymbol{x};\boldsymbol{\mu}_j,\boldsymbol{\Sigma}_j)
\end{aligned}\tag{3}$$
求解 #
现在模型有了,但是未知的参数有$\pi_j,\boldsymbol{\mu}_j,\boldsymbol{\Sigma}_j$,怎么确定它们呢?
理想的方法是最大似然估计,然而它并没有解析解,因而需要转化为一个EM过程,但即使这样,求解过程也比较难理解(涉及到行列式的求导)。这里给出一个比较简单明了的推导,它基于这样的一个事实——对于正态分布来说,最大似然估计跟前两阶矩的矩估计结果是一样的。(相信我,这应该是你能找到的最简单的GMM推导之一。)
说白了,$\boldsymbol{\mu}_j,\boldsymbol{\Sigma}_j$不就是正态分布的均值(向量)和(协)方差(矩阵)嘛,我直接根据样本算出对应的均值和方差不就行了吗?没那么简单,因为我们所假设的是一个正态分布的混合模型,如果直接算它们,得到的也只是混合的均值和方差,没法得到每一类的正态分布$p(\boldsymbol{x}|j)$的均值和方差。
不过我们可以用贝叶斯公式转化一下,首先我们有
$$p(j|\boldsymbol{x})=\frac{p(\boldsymbol{x}|j)p(j)}{p(\boldsymbol{x})}=\frac{\pi_j N(\boldsymbol{x};\boldsymbol{\mu}_j,\boldsymbol{\Sigma}_j)}{\sum\limits_{j=1}^k\pi_j N(\boldsymbol{x};\boldsymbol{\mu}_j,\boldsymbol{\Sigma}_j)}\tag{4}$$
比如对于均值向量,我们有
$$\boldsymbol{\mu}_j = \int p(\boldsymbol{x}|j)\boldsymbol{x}d\boldsymbol{x}=\int p(\boldsymbol{x}) \frac{p(j|\boldsymbol{x})}{p(j)}\boldsymbol{x}d\boldsymbol{x}=E\left[\frac{p(j|X)}{p(j)}X\right]\tag{5}$$
这里$E[]$的意思是对所有样本求数学期望,那么我们就可以得到
$$\boldsymbol{\mu}_j = \frac{1}{n}\sum\limits_{i=1}^n \frac{p(j|\boldsymbol{x}_i)}{p(j)}\boldsymbol{x}_i = \frac{1}{\pi_j n}\sum\limits_{i=1}^np(j|\boldsymbol{x}_i)\boldsymbol{x}_i\tag{6}$$
其中$p(j|\boldsymbol{x})$的表达式在$(4)$已经给出。类似地,对于协方差矩阵,我们有
$$\boldsymbol{\Sigma}_j = \frac{1}{\pi_j n}\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)(\boldsymbol{x}_i-\boldsymbol{\mu}_j)(\boldsymbol{x}_i-\boldsymbol{\mu}_j)^{\top}\tag{7}$$
然后
$$\pi_j = p(j) = \int p(j|\boldsymbol{x})p(\boldsymbol{x})d\boldsymbol{x}=E\left[p(j|X)\right]\tag{8}$$
所以
$$\pi_j = \frac{1}{n}\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)\tag{9}$$
理论上,我们需要求解$(4),(6),(7),(9)$构成的一个巨大的方程组,但这样是难以操作的,因此我们可以迭代求解,得到迭代算法:
$$\text{EM算法1}:\left\{\begin{aligned}
&p(j|\boldsymbol{x}_i) \leftarrow \frac{\pi_j N(\boldsymbol{x}_i;\boldsymbol{\mu}_j,\boldsymbol{\Sigma}_j)}{\sum\limits_{j=1}^k\pi_j N(\boldsymbol{x}_i;\boldsymbol{\mu}_j,\boldsymbol{\Sigma}_j)}\\
&\boldsymbol{\mu}_j \leftarrow \frac{1}{\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)}\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)\boldsymbol{x}_i\\
&\boldsymbol{\Sigma}_j \leftarrow \frac{1}{\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)}\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)(\boldsymbol{x}_i-\boldsymbol{\mu}_j)(\boldsymbol{x}_i-\boldsymbol{\mu}_j)^{\top}\\
&\pi_j \leftarrow \frac{1}{n}\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)
\end{aligned}\right.$$
其中为了突出加权平均的特点,上述迭代过程先将$(9)$式作了恒等变换然后代入$(6),(7)$式。在上述迭代过程中,第一式称为$E$步,后三式称为$M$步,整个算法就叫做EM算法。下面放一张网上搜索而来的动图来展示GMM的迭代过程,可以看到GMM的好处是能识别出一般的二次曲面形状的类簇,而K-Means只能识别出球状的。
约简 #
在Capsule中实际上使用了一种更加简单的GMM形式,在前面的讨论中,我们使用了一般的正态分布,也就是$(2)$式,但这样要算矩阵的逆和行列式,计算量颇大。一个较为简单的模型是假设协方差矩阵是一个对角阵$\boldsymbol{\Sigma}_j = \text{diag}\boldsymbol{\sigma}^2_j$,$\boldsymbol{\sigma}^2_j$是类别$j$的方差向量,那么$\boldsymbol{\sigma}_j$也就是标准差向量了,而$\boldsymbol{\sigma}_j^{l}$表示该标准差向量的第$l$个分量。这样相当于将$\boldsymbol{x}$的各个分量解耦了,认为各个分量是独立的,$(2)$式就变为
$$N(\boldsymbol{x};\boldsymbol{\mu}_j,\boldsymbol{\sigma}^2_j)=\prod_{l=1}^d\frac{1}{\sqrt{2\pi}\sigma_j^{l}}\exp\left(-\frac{1}{2(\sigma_j^{l})^2}(x^{l}-\mu_j^{l})^2\right)\tag{10}$$
而迭代过程也有所简化:
$$\text{EM算法2}:\left\{\begin{aligned}
&p(j|\boldsymbol{x}_i) \leftarrow \frac{\pi_j N(\boldsymbol{x}_i;\boldsymbol{\mu}_j,\boldsymbol{\sigma}^2_j)}{\sum\limits_{j=1}^k\pi_j N(\boldsymbol{x}_i;\boldsymbol{\mu}_j,\boldsymbol{\sigma}^2_j)}\\
&\boldsymbol{\mu}_j \leftarrow \frac{1}{\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)}\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)\boldsymbol{x}_i\\
&\boldsymbol{\sigma}^2_j \leftarrow \frac{1}{\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)}\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)(\boldsymbol{x}_i-\boldsymbol{\mu}_j)^2\,[\text{逐位平方}]\\
&\pi_j \leftarrow \frac{1}{n}\sum\limits_{i=1}^n p(j|\boldsymbol{x}_i)
\end{aligned}\right.$$
更简单些 #
如果所有的$\sigma_{j}^{l}$都取同一个常数$\sigma$呢?这就得到
$$N(\boldsymbol{x};\boldsymbol{\mu}_j,\sigma)=\frac{1}{\sqrt{2\pi}\sigma^d}\exp\left(-\frac{1}{2\sigma^2}\Vert \boldsymbol{x}-\boldsymbol{\mu}_j\Vert^2\right)\tag{11}$$
这样整个分布就更为简单了,有意思的是,在指数的括号内出现了欧氏距离。
更极端地,我们让$\sigma\to 0$呢?这时指数内的括号为负无穷大,不难证明:对于每个$\boldsymbol{x}_i$,只有$\Vert \boldsymbol{x}_i-\boldsymbol{\mu}_j^2\Vert^2$的那个$N(\boldsymbol{x}_i;\boldsymbol{\mu}_j,\sigma^2)$占主导,这时候根据$(4)$式,$p(j|\boldsymbol{x}_i)$非零即1(即使得$\Vert \boldsymbol{x}_i-\boldsymbol{\mu}_j^2\Vert^2$最小的那个$j$的$p(j|\boldsymbol{x}_i)$为1,其余为0),这表明任意一个点只属于距离它最近的那个聚类中心,这就跟使用欧氏距离的K-Means一致了,所以说,基于欧氏距离的K-Means可以看作是GMM的一个极限。
新版路由 #
言归正传,还是说回Capsule。我们说《Matrix Capsules with EM Routing》中用GMM算法完成了聚类过程,现在就来详细看看是怎么做的。
矩阵->向量 #
不得不说,新论文里边的符号用得一塌糊涂,也许能够在一堆混乱的符号中看到真理才是真正的大牛吧。这里结合网上的一些科普资料以及作者自己的阅读,给出一些理解。
首先,我们用一个矩阵$\boldsymbol{P}_i$来表示第$l$层的Capsule,这一层共有$n$个Capsule,也就是$i=1,\dots,n$;用矩阵$\boldsymbol{M}_j$来表示第$l+1$层的Capsule,这一层共有$k$个Capsule,也就是聚为$k$类,$j=1,\dots,k$。论文中Capsule的矩阵是$4\times 4$的,称之为Pose矩阵。然后呢,就可以开始GMM的过程了,在做GMM的时候,又把矩阵当成向量了,所以在EM路由那里,$\boldsymbol{P}_i$就是向量,即$d=16$。整个过程用的是简化版的GMM,也就是把协方差矩阵约定为一个对角阵。
所以根据前面的讨论,可以得到新的动态路由算法
$$\text{新动态路由1}:\left\{\begin{aligned}
&p_{ij} \leftarrow N(\boldsymbol{P}_i;\boldsymbol{\mu}_j,\boldsymbol{\sigma}^2_j)\\
&R_{ij} \leftarrow \frac{\pi_j p_{ij} }{\sum\limits_{j=1}^k\pi_j p_{ij} },\,\,r_{ij}\leftarrow \frac{R_{ij}}{\sum\limits_{i=1}^n R_{ij}}\\
&\boldsymbol{M}_j \leftarrow \sum\limits_{i=1}^n r_{ij}\boldsymbol{P}_i\\
&\boldsymbol{\sigma}^2_j \leftarrow \sum\limits_{i=1}^n r_{ij}(\boldsymbol{P}_i-\boldsymbol{M}_j)^2\\
&\pi_j \leftarrow \frac{1}{n}\sum\limits_{i=1}^n R_{ij}
\end{aligned}\right.$$
这里记了$p_{ij}=N(\boldsymbol{x}_i;\boldsymbol{\mu}_j,\boldsymbol{\sigma}^2_j),R_{ij}=p(j|\boldsymbol{x}_i)$,符号尽量跟原论文一致,方便大家对比原论文。这里的动态路由的思想跟《Dynamic Routing Between Capsules》的是一致的,都是将$l+1$层的Capsule作为$l$层Capsule的聚类中心,只是聚类的方法不一样而已。
激活值 #
在《Dynamic Routing Between Capsules》一文中,是通过向量的模长来表示该特征的显著程度,那么在这里还可以这样做吗?答案是否定的。因为我们使用了GMM进行聚类,GMM是基于加权的欧氏距离(本质上还是欧氏距离),用欧氏距离进行聚类的一个特点就是聚类中心向量是类内向量的(加权)平均(从上面$\boldsymbol{M}_j$的迭代公式就可以看出),既然是平均,就不能体现“小弟越多,势力越大”的特点,这在《再来一顿贺岁宴:从K-Means到Capsule》中就已经提到过了。
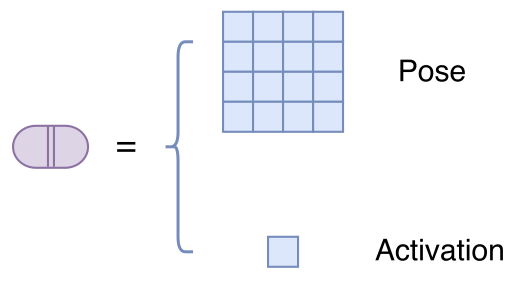
既然Capsule的模长已经没法衡量特征的显著性了,那么就只好多加一个标量$a$来作为该Capsule的显著性。所以,这篇论文中的Capsule,实际上是“一个矩阵 + 一个标量”,这个标量被论文称为“激活值”,如图:
作为Capsule的显著程度,$a_j$最直接的选择应该就是$\pi_j$,因为$l+1$层的Capsule就是聚类中心而$\pi_j$就代表着这个类的概率。然而,我们却不能选择$\pi_j$,原因有两个:
1、$\pi_j$是归一化的,而我们希望得到的只不过是特征本身的显著程度,而不是跟其他特征相比后的相对显著程度(更通俗点,我们希望做多个二分类,而不是一个多分类,所以不需要整体归一化);
2、$\pi_j$确实能反映该类内“小弟”的多少,但人多不一定力量大,还要团结才行。
那么这个激活值应该怎么取呢?论文给出的公式是
$$a_j=logistic\left(\lambda\left(\beta_a-\beta_u\sum\limits_i R_{ij}-\sum\limits_h cost_j^h\right)\right)\tag{12}$$
我相信很多读者看到这个公式和论文中的“推导”后,还是不知所云。事实上,这个公式有一个非常漂亮的来源——信息熵。
现在我们用GMM来聚类,结果就是得到一个概率分布$p(\boldsymbol{X}|j)$来描述一个类,那么这个类的“不确定性程度”,也就可以衡量这个类的“团结程度”了。说更直白一点,“不确定性”越大(意味着越接近均匀分布),说明这个类可能还处于动荡的、各自为政的年代,此时激活值应该越小;“不确定性”越小(意味着分布越集中),说明这个类已经团结一致步入现代化,此时激活值应该越大。
因此可以用不确定性来描述这个激活值,而我们知道,不确定性是用信息熵来度量的,所以我们写出
$$\begin{aligned}S_j =& - \int p(\boldsymbol{x}|j)\ln p(\boldsymbol{x}|j)d\boldsymbol{x}\\
=& - \frac{1}{p(j)}\int p(j|\boldsymbol{x})p(\boldsymbol{x})\ln p(\boldsymbol{x}|j)d\boldsymbol{x}\\
=&- \frac{1}{p(j)} E\left[p(j|\boldsymbol{x})\ln p(\boldsymbol{x}|j)\right]\\
=&-\frac{1}{n\pi_j}\sum\limits_{i=1}^n R_{ij}\ln p_{ij}\\
=&-\frac{1}{\sum\limits_{i=1}^n R_{ij}}\sum\limits_{i=1}^n R_{ij}\ln p_{ij}\\
=&-\sum\limits_{i=1}^n r_{ij}\ln p_{ij}\end{aligned}\tag{13}$$
这就是论文中的那个$cost_j^h$,所以论文中的$cost$就是熵,多直观清晰的含义!而且熵越小越好,这也是多自然的逻辑!(为什么不直接积分算出正态分布的熵,而是要这样迂回地算?因为直接积分算出来是理论结果,我们这里要根据这批数据本身算出一个关于这批数据的实际结果)。
注:如果读者不能很好地理解采样计算,请阅读《变分自编码器(二):从贝叶斯观点出发》中的《数值计算vs采样计算》一节。
经过化简,结果是(原论文计算结果应该有误)
$$S_j = \frac{d}{2}+\left(\sum\limits_{l=1}^d \ln \boldsymbol{\sigma}_j^l+\frac{d}{2}\ln (2\pi)\right)\sum\limits_i r_{ij}\tag{14}$$
补充推导:这里的假设是$p_{ij}$对应了一个$d$元的独立的正态分布,所以只需要求出每一元的熵然后求和:
$$\begin{aligned}S_j^l =& \sum_{i} - r_{ij} \ln p_{ij}^l\\
=&\sum_{i} - r_{ij} \ln \left[\frac{1}{\sqrt{2\pi}\boldsymbol{\sigma}_j^l}\exp\left(-\frac{(\boldsymbol{x}_i^l-\boldsymbol{\mu}_{j}^l)^2}{2(\boldsymbol{\sigma}_{j}^l)^2}\right)\right]\\
=&\left(\frac{1}{2}\ln 2\pi + \ln\boldsymbol{\sigma}_j^l\right)\sum_{i} r_{ij}+\frac{\sum\limits_{i}r_{ij}\left(\boldsymbol{x}_i^l-\boldsymbol{\mu}_{j}^l\right)^2}{2(\boldsymbol{\sigma}_{j}^l)^2}
\end{aligned}$$
注意到最后一项的分子实际上就是方差的定义计算公式,而分母是方差的两倍,所以最后一项就是“方差/方差”再除以2,即
$$S_j^l = \sum_{i} - r_{ij} \ln p_{ij}^l=\left(\frac{1}{2}\ln 2\pi + \ln\boldsymbol{\sigma}_j^l\right)\sum_{i} r_{ij}+\frac{1}{2}$$
于是
$$S_j = \sum_{l=1}^d S_j^l =\left(\frac{d}{2}\ln 2\pi + \sum_{l=1}^d\ln\boldsymbol{\sigma}_j^l\right)\sum_{i} r_{ij}+\frac{d}{2}$$
因为熵越小越显著,所以我们用$-S_j$来衡量特征的显著程度,但又想将它压缩为0~1之间。那么可以对它做一些简单的尺度变换后用sigmoid函数激活:
$$a_j = sigmoid\left( \lambda \left( \beta_a - \left(\beta_u+\sum\limits_{l=1}^d \ln \boldsymbol{\sigma}_j^l \right)\sum\limits_i r_{ij}\right)\right)\tag{15}$$
$(15)$式和$(13)$式基本是等价的,上式相当于$-S_j$和$\pi_j$的加权求和,也就是综合考虑了$-S_j$(团结)和$\pi_j$(人多)。其中$\beta_a,\beta_u$通过反向传播优化,而$\lambda$则随着训练过程慢慢增大(退火策略,这是论文的选择,我认为是不必要的)。$\beta_a,\beta_u$可能跟$j$有关,也就是可以为每个上层胶囊都分配一组训练参数$\beta_a,\beta_u$。说“可能”是因为论文根本就没说清楚,或许读者可以按照自己的实验和需求调整。
路由现 #
有了$a_j$的公式后,因为我们前面也说$a_j$和$\pi_j$有一定共同之处,它们都是类的某种权重,于是为了使得整个路由流程更紧凑,Hinton干脆直接用$a_j$替换掉$\pi_j$,这样替换虽然不能完全对应上原始的GMM的迭代过程,但含义是类似的,而且也能收敛。于是现在得到更正后的动态路由
$$\text{新动态路由2}:\left\{\begin{aligned}
&p_{ij} \leftarrow N(\boldsymbol{P}_i;\boldsymbol{\mu}_j,\boldsymbol{\sigma}^2_j)\\
&R_{ij} \leftarrow \frac{a_j p_{ij} }{\sum\limits_{j=1}^k a_j p_{ij} },\,\,r_{ij}\leftarrow \frac{R_{ij}}{\sum\limits_{i=1}^n R_{ij}}\\
&\boldsymbol{M}_j \leftarrow \sum\limits_{i=1}^n r_{ij}\boldsymbol{P}_i\\
&\boldsymbol{\sigma}^2_j \leftarrow \sum\limits_{i=1}^n r_{ij}(\boldsymbol{P}_i-\boldsymbol{M}_j)^2\\
& cost_j \leftarrow \left(\beta_u+\sum\limits_{l=1}^d \ln \boldsymbol{\sigma}_j^l \right)\sum\limits_i r_{ij} \\
& a_j \leftarrow sigmoid\left( \lambda \left(\beta_a - cost_j\right)\right)
\end{aligned}\right.$$
忍住别晕倒,已经很接近终点了。现在这个算法基本上已经没有问题了,但是你会发现,如果多层Capsule联合在一起的话,我们就漏掉了一个细节:$\boldsymbol{P}_i$就是上一层的capsule矩阵,我们已经用上了,但是上一层的激活值(记为$a^{last}_i$)呢?别忘了在矩阵Capsule中,每一个Capsule都是矩阵+标量,只用矩阵显然是不完整的,而Hinton将激活值插入到了$r_{ij}\leftarrow \frac{R_{ij}}{\sum\limits_{i=1}^n R_{ij}}$这一步,所以:
$$\text{新动态路由3}:\left\{\begin{aligned}
&p_{ij} \leftarrow N(\boldsymbol{P}_i;\boldsymbol{\mu}_j,\boldsymbol{\sigma}^2_j)\\
&R_{ij} \leftarrow \frac{a_j p_{ij} }{\sum\limits_{j=1}^k a_j p_{ij} },\,\,r_{ij}\leftarrow \frac{a^{last}_i R_{ij}}{\sum\limits_{i=1}^n a^{last}_i R_{ij}}\\
&\boldsymbol{M}_j \leftarrow \sum\limits_{i=1}^n r_{ij}\boldsymbol{P}_i\\
&\boldsymbol{\sigma}^2_j \leftarrow \sum\limits_{i=1}^n r_{ij}(\boldsymbol{P}_i-\boldsymbol{M}_j)^2\\
& cost_j \leftarrow \left(\beta_u+\sum\limits_{l=1}^d \ln \boldsymbol{\sigma}_j^l \right)\sum\limits_i r_{ij} \\
& a_j \leftarrow sigmoid\left( \lambda \left(\beta_a - cost_j\right)\right)
\end{aligned}\right.$$
这应该就是论坛中的新的动态路由算法了——如果我没理解错的话——因为原论文实在太难看懂。最后这个细节相信很多读者都没有留意到。为什么呢?因为论文中的符号使用是这样的:
(意不意外,惊不惊喜?)
还有一点点~~读者可以留意到,其实按照我们的定义应该有$\sum\limits_i r_{ij}=1$,为什么不直接化简呢?其实我也不知道为什么,论文中的$cost_j$其实不是用$r_{ij}$,而是$a^{last}_i R_{ij}$!也就是
$$\text{新动态路由4}:\left\{\begin{aligned}
&p_{ij} \leftarrow N(\boldsymbol{P}_i;\boldsymbol{\mu}_j,\boldsymbol{\sigma}^2_j)\\
&R_{ij} \leftarrow \frac{a_j p_{ij} }{\sum\limits_{j=1}^k a_j p_{ij} },\,\,r_{ij}\leftarrow \frac{a^{last}_i R_{ij}}{\sum\limits_{i=1}^n a^{last}_i R_{ij}}\\
&\boldsymbol{M}_j \leftarrow \sum\limits_{i=1}^n r_{ij}\boldsymbol{P}_i\\
&\boldsymbol{\sigma}^2_j \leftarrow \sum\limits_{i=1}^n r_{ij}(\boldsymbol{P}_i-\boldsymbol{M}_j)^2\\
& cost_j \leftarrow \left(\beta_u+\sum\limits_{l=1}^d \ln \boldsymbol{\sigma}_j^l \right)\sum\limits_i a^{last}_i R_{ij} \\
& a_j \leftarrow sigmoid\left( \lambda \left(\beta_a - cost_j\right)\right)
\end{aligned}\right.$$
好吧,我已经无力吐槽了,Hinton爱怎么玩就怎么玩吧。就算可以牵强解释下去(也许大概意思就是这一层的激活值应该还要受到上一层的激活值的调控吧),也没有什么启发意义了。
权重矩阵 #
最后的最后,跟前一篇文章一样,给每对指标$(i,j)$配上一个权重矩阵$\boldsymbol{W}_{ij}$(称为视觉不变矩阵),得到“投票矩阵”$\boldsymbol{V}_{ij}=\boldsymbol{P}_{i}\boldsymbol{W}_{ij}$,然后再进行动态路由,得到最终的动态路由算法
$$\text{新动态路由(完整)}:\left\{\begin{aligned}
&p_{ij} \leftarrow N(\boldsymbol{V}_{ij};\boldsymbol{\mu}_j,\boldsymbol{\sigma}^2_j)\\
&R_{ij} \leftarrow \frac{a_j p_{ij} }{\sum\limits_{j=1}^k a_j p_{ij} },\,\,r_{ij}\leftarrow \frac{a^{last}_i R_{ij}}{\sum\limits_{i=1}^n a^{last}_i R_{ij}}\\
&\boldsymbol{M}_j \leftarrow \sum\limits_{i=1}^n r_{ij}\boldsymbol{V}_{ij}\\
&\boldsymbol{\sigma}^2_j \leftarrow \sum\limits_{i=1}^n r_{ij}(\boldsymbol{V}_{ij}-\boldsymbol{M}_j)^2\\
& cost_j \leftarrow \left(\beta_u+\sum\limits_{l=1}^d \ln \boldsymbol{\sigma}_j^l \right)\sum\limits_i a^{last}_i R_{ij} \\
& a_j \leftarrow sigmoid\left( \lambda \left(\beta_a - cost_j\right)\right)
\end{aligned}\right.$$
结语 #
评价 #
经过这样一番分析,应该可以感觉到这个新版的Capsule及其路由算法并不复杂。新论文的要点是使用了GMM来完成聚类过程,GMM是一个基于概率模型的聚类算法,紧抓住“概率模型”这一特性,寻找概率相关的量,就不难理解$a_j$表达式的来源,这应该是理解整篇论文最困难的一点;而用矩阵代替向量,应该只是一种降低计算量和参数量的方案,并无本质变化。
只不过新论文传承了旧论文的晦涩难懂的表达方式,加上混乱的符号使用,使得我们的理解难度大大增加,再次诟病作者们的文笔。
当然,论文中还是有些难懂的、不知思路的东西,比如上面说的$cost_j$的$r_{ij}$就被替换了$a^{last}_i R_{ij}$,如果大家有什么更有启发性的思路,欢迎留言讨论。
感想 #
到现在,总算是把《Matrix Capsules with EM Routing》梳理清楚了,至于代码就不写了,因为事实上我个人并不是特别喜欢这个新的Capsule和动态路由,不想再造轮子了。
这是我的关于Capsule理解的第三篇文章。相对于科学空间其他文章而言,这三篇文章的篇幅算得上是“巨大”,它们承载了我对Capsule的思考和理解。每一篇文章的撰写都要花上好几天的时候,试图尽可能理论和通俗文字相结合,尽可能把前因后果都梳理清楚。希望这些文字能帮助读者更快速地理解Capsule。当然,作者水平有限,如果有什么误导之处,欢迎留言批评。
当然,更希望Capsule的作者们能用更直观、更具启发性的语言来介绍他们的新理论,这就省下了我们这些科普者的不少功夫了。毕竟Capsule有可能真的是深度学习的未来,怎可如此模糊呢?
转载到请包括本文地址:https://kexue.fm/archives/5155
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Mar. 02, 2018). 《三味Capsule:矩阵Capsule与EM路由 》[Blog post]. Retrieved from https://kexue.fm/archives/5155
@online{kexuefm-5155,
title={三味Capsule:矩阵Capsule与EM路由},
author={苏剑林},
year={2018},
month={Mar},
url={\url{https://kexue.fm/archives/5155}},
}











July 8th, 2018
作者,请问动态路由算法转换为K-means也能计算矩阵的值吗?必须使用GMM吗?
k-means亦可,参考
https://kexue.fm/archives/5112
September 25th, 2018
作者写的很好,我读的时候也觉得R_ij和r_ij那里很怪,对于第L+1层的某个capsule,聚类完成后,聚类中心为u_j,这可以认为是多维高斯分布的中心,这个中心确实不能表达聚集的程度,但是加上算出的方差信息后,我觉得就可以表达出聚集的程度了,似乎不需要另外设计激活值a_j
谢谢。只考虑方差也不够的,还要表示出“多少”,也就是说“人多”且“团结一致”才“力量大”。
感谢您的回复,p_j就可以反映"多少"啊,p_j越大,说明模型拟合的越好。方差sigma_j向量的模长越小,则说明整体上数据更集中,可以反映出"团结一致",概率论比较差,作者认为哪里不合理呢?确实可以反映出"人多"且"团结一致"啊.
$p_j$是哪个?
October 7th, 2018
[...]三味Capsule:矩阵Capsule与EM路由[...]
October 7th, 2018
您好,
首先感谢笔者的无私奉献,关于(14)式子我也思考了一下,我认为原文是对的。
原文并没有说$r_{ij}$是归一化的,因此$\frac{\sum\limits_{i}r_{ij}\left(\mathbb{x}_i^l-\mathbb{\mu}_{j}^l\right)^2}{2(\mathbb{\sigma}_{j}^l)^2}$ 的分母并不是方差,而是方差的$\sum\limits_{i}r_{ij}$倍,因此原文推导我认为是正确的。
Zewen
10/7/2018
sorry笔误,第二行应该是“分子”,不是“分母”
这样理解也无妨,不过我想的是提供一种自上而下的理解而已。
反正这个routing不管怎么解释都莫名其妙的~
February 5th, 2020
文章中说sigma\r_{ij}\是分配到j capsule的数据的数量,这个怎么理解呢?具体的表达式可以为sigma\R_(ij}\吗?
补充一下,这个数据的数量是不是可以理解为您说的“小弟”?
不知道你想表达什么,能再说清楚一点?
不好意思哈,我之前讲的不太清楚。原文《MATRIX CAPSULES WITH EM ROUTING》的第3页公式(1)下面一行指明了"where $\sum\limits_{i}r_{ij}$ is the amount of data assigned to $j$ " 这个怎么理解呢?感觉跟您说的不太一致,如果真的如原文表示的分配到capsule $j$的数量,这个数量是不是可以理解为您在博客中所描述的类内的“小弟”的数量?
原文说得不清不楚乱七八糟的,就别过于纠结原文了。以原文给出的Procedure 1的流程图为准,结合网上开源的代码,自己理解就好。
February 5th, 2020
这篇文章写得真好~非常感谢苏老师的分享。
February 11th, 2020
最新研究,Hinton 说:「忘了前面所有版本的 Capsule,它们都是有误的,2019 年这个版本是对的。」,期待苏老师分析 Stacked Capsule Autoencoders
没什么动力了(捂脸),有机会再看看吧~
March 2nd, 2020
苏神什么时候解读一下hinton最新版的capsule,个人感觉有点意思,但是受限于自身水平搞不太懂。。
目前对capsule没什么兴趣~
August 3rd, 2020
太感谢您了,是我看过的讲GMM的最好的文章,
顺便测试一下latex$e=mc^2$
$$F= \int_{x_0}^{x_1}xy dx$$
March 4th, 2021
非常感谢您深入浅出的讲解,我很快就看明白了,不知道能否请您讲解下第三篇的capsule,限于自身水平看的云里雾里的。