科学空间|Scientific Spaces

我小时候一直有个疑问：

直升机上的螺旋桨能不能用来挡雨？

一般的螺旋桨是若干个“条状”物通过旋转对称而形成的，也就是说，它并非一个面，按常理来说，它是没办法用来挡雨的。但是，如果在高速旋转的情况下，甚至假设旋转速度可以任意大，那么我们任意时刻都没有办法穿过它了，这种情况下，它似乎与一个实在的面无异？

力的无穷分解

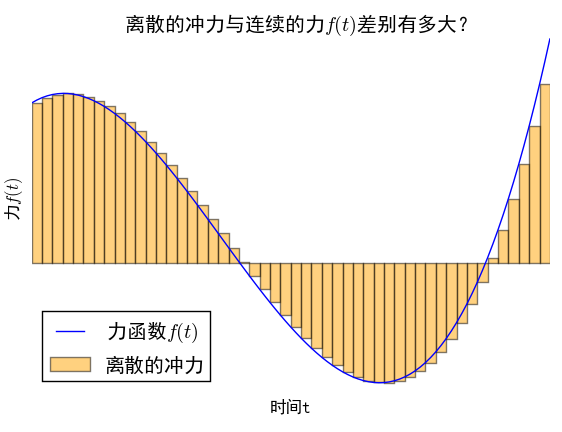
当然，以上只是笔者小时候的一个“异想天开”的念头，读者不必较真。不过，这个疑问跟本文有什么联系呢？我们在研究振动问题之时，通常会遇到在变力的作用下的受迫振动问题，已知变力是时间的函数，比如$f(t)$，然而，虽然知道$f(t)$的具体形式，但是由于$f$的非线性性，加上外力之后的运动，不一定容易求解。然而，如果可以将一个变化的力分段为无数个无穷小时间内的恒力（冲力），那么我们就可以分段讨论我们要研究的运动，而通常来说，恒力的问题会比变力容易。将一个变力离散化，然后再取极限，那么是不是跟原来在变力下的运动是一样的呢？这跟文章开头的疑问有着类似的思想——离线的极限，跟连续本身，是不是等价的？

而让人惊喜的是，在通常的物理系统中，将力分段为无数个小区间内的恒力的做法，能够导致正确的答案，而且，这恰好是线性常微分方程的格林函数法。下面我们来分析这一做法。

点击阅读全文...

本文很荣幸得到了高教社的王超编辑（新浪微博 @朗道集结号 ）在微信上的推荐，在此表示十分的感谢。

朗道集结号
朗道、费曼、薛定谔、泡利、狄拉克、温伯格……大师在这里等着你，微信号：ldjjhwx

事实上，取这个标题，有点狂妄自大、班门弄斧的感觉。原因之一是我自己并非物理专业学生，也没有学好物理。再者，我自己也没有读过多少费曼和朗道的书，谈不上“饱读”费曼朗道，又何以指导大家呢？

但是，结合自己在阅读他们的著作的感受，以及自己学习科学的过程，谈谈我对他们的著作的看法。

什么才是最简洁的方式？

相信不少读者觉得朗道的教程比费曼的讲义要深，感觉朗道的书总有大量的数学公式，而费曼的书则轻松一些。笔者开始也有这样的感觉，但是慢慢读下去，才感到费曼的书甚至比朗道的困难。

在进入讨论之前，我们不妨先想一下：什么才是理解物理的最简洁方式？数学越复杂，就越不好吗？

点击阅读全文...

为了形象地展示为什么有些系统需要旋转720度而不是360度才能恢复原状，费曼想到了一个“茶杯法”。看了“茶杯法”的步骤之后，我突然想起了电影《太极1》的梁小龙的一个端药镜头，正好对应着费曼的“茶杯法”，遂把镜头剪了出来，供大家欣赏。

请仔细观察梁小龙的手转了多少圈？

点击阅读全文...

在线阅读地址：
http://www.feynmanlectures.caltech.edu/

刚在浏览《朗道集结号》的微博时，发现了这一造福大众的消息。难得的是，这个在线版通过MathJax使用Latex排版，阅读效果完全丝毫不输于纸质版的，还可以自由复制。只是遗憾只有英文版的，也许有一天心血来潮，我也弄个在线的中文版出来，呵呵。一切皆有可能。

费曼的物理讲义是一套地地道道的物理书，它是一次美妙的物理之旅。纵使你可能已经读过相当多的物理教材，但是读读费曼的讲义还是大有裨益的，它给我们讲述了什么才是物理，怎么才能学物理。

上一篇文章里我已经从我自己的理解角度简单说了一下场论的必要性，这次让我们再次谈到这个话题，企图在文字层面上得到更深入的认识。

上一两周的时间，我一直在找资料，主要是线性引力的资料，并且发现了很多有趣的东西，在此一并与大家分享一下。首先，当我在Google中输入“线性引力”时，我发现了一本“奇书”，一本名副其实的“巨著”——《引力论》！洋洋1300多页的大作，三位“超级巨星”——C.W.麦思纳（Charles W.Misner）、K.S.索恩（Kip S.Thorne）、J.A.惠勒（John Archibald Wheeler）——联合编写，恐怕再也找不到哪本书可以PK它的“全明星阵容”了。该书英文名为Gravitation，中文是由台湾翻译的，繁体中文版。全书讲述了引力的研究历史和发展情况，更重要的是几乎每一处历史都给出了数学论证！最最重要的，作者惠勒还是跟爱因斯坦同一个研究时代的人，我们可以最真实的感受到那年代的研究。看到这里，我就迫不及待地想买了，由于各种原因，我们很难买到，到图书馆找，发现有英文版的，就马上借过来了，另外因为买不到中文版，我只好到网上买了电子版，然后打印出来了。不过不是很清晰，而且自我感觉中文翻译不是很好（当然，已经够我们阅读了）。

点击阅读全文...

传说费曼讲课很精彩，但他是上个世纪的人，所以也就没有多少视频保留下来。但是网上还是存有一些，有兴趣的读者可以收藏。

费曼讲座——光、电子、路径积分（无字幕）
http://v.youku.com/v_show/id_XNjAyMzU4ODg=.html

http://v.youku.com/v_show/id_XNjAyMzQ4NzI=.html

http://v.youku.com/v_show/id_XNTQzMTEyNTA4.html

http://v.youku.com/v_show/id_XNjAyMzQ4MzI=.html

点击阅读全文...

自从了解了费曼积分法之后，我就一直想着用费曼积分法来求高斯积分$\int_0^{\infty} e^{-x^2}dx=\frac{\sqrt{\pi}}{2}$这个神奇的积分，但一直无果。在《数学桥》里边，作者是通过将其转变为二重积分来解决的，简洁而巧妙。但是为了显示费曼积分法的威力，我一直想找到高斯积分的其他求法。上星期在《数学物理方法》中看到作者用拉普拉斯变换求出了该积分，眼睛不禁为之一亮，不过这属于积分变换内容，属于“积分符号内取积分”的技巧，在此不作讨论。今天在网上查找资料时，在“赵洁”的一篇论文《含参变量积分》中，看到了一种属于费曼积分法范畴内的方法，特与大家分享。

从“事后分析”来看，高斯积分的结果涉及到了$\sqrt{\pi}$这个量，一般来说我们常见的公式出现$\pi$的不少，可是几乎没有出现$\sqrt{\pi}$的，所以一般来说我们都将它平方。我们引入
$$f(x)=(\int_0^x e^{-t^2}dt)^2$$

点击阅读全文...

在本系列的第五篇文章中，BoJone导出了一些看似不合理的公式，而且并没有说明它的应用和来源。其实，这些都是我在研究以下积分的时候总结出来的：

$$\int_{-\infty}^{+\infty} \frac{\cos x}{a^2+x^2}dx$$

点击阅读全文...