把地球放到“宇宙中心”...
By 苏剑林 | 2010-02-21 | 32545位读者 | 引用“n次方程有n个根”的证明
By 苏剑林 | 2010-02-27 | 75850位读者 | 引用(原创)切抛物线法解方程
By 苏剑林 | 2010-03-06 | 35355位读者 | 引用牛顿法使用的是函数切线的方程的零点来逼近原函数的零点,他所使用的是“切直线”,要是改为同曲率的“切抛物线”,则有更稳定的收敛效果以及更快的收敛速度
设函数$y=f(x)$在$(x_0,y_0)$处有一条“切抛物线”$y=ax^2+bx+c$,则应该有
$a(x_0+\Delta x)^2+b(x_0+\Delta x)+c=f(x_0+\Delta x)$-------(A)
$ax_0^2+bx_0+c=f(x_0)$-------(B)
$a(x_0-\Delta x)^2+b(x_0-\Delta x)+c=f(x_0-\Delta x)$-------(C)
其中$lim_{\Delta x->0}$
解答不等式的误区...
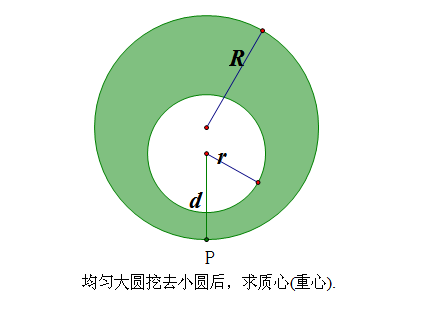
By 苏剑林 | 2010-05-02 | 37107位读者 | 引用问世间质心(重心)知多少
By 苏剑林 | 2010-07-26 | 49925位读者 | 引用眼见未必为实——“视超光速”现象的产生
By 苏剑林 | 2010-06-05 | 72766位读者 | 引用威力巨大的“有向线段”
By 苏剑林 | 2010-06-27 | 22056位读者 | 引用《向量》系列——1.向心力公式证明
By 苏剑林 | 2010-07-15 | 63110位读者 | 引用向量在几何和物理中都有极其重要的作用,现在就让我们来看如何用向量研究物理中的圆周运动。
首先我们必须了解一些基础:
1.在向量中,只要一条“向径”($\vec{r}$)就可以描述出物体的运动,而不需要建立坐标系。这就是向量应用于物理的原因:物理定律不应该依赖于坐标系,而向量恰恰也不依赖于坐标系!
2.牛顿第二定律:$\vec{F}=m\vec{a}$
3.以及一些向量的微积分运算等(可以查阅维基百科或者相关资料)
在下面及以后的文章描述中,为了大家的阅读方便,把向量写成$\vec{r}$的形式,而非把字母加粗。一般情况下,在本站的描述中,有$|\vec{r}|=r,|\dot{\vec{r}}|=v,|\ddot{\vec{r}}|=a$。但是,$\dot{r}=\frac{d|\vec{r}|}{dt} != |\dot{\vec{r}}|$










最近评论