在讨论了倒立单摆的相关分析之后,胡雄大哥(笔者的一位好友)提出了一个问题:一根均匀杆,当然质量不可忽略,只有一个力(简单起见,可以先假设为恒力)作用在其中一个点上(简单起见,可以假设为端点),那么杆是怎么运动的?
其实笔者学了不少的经典力学,也分析了不少问题,但就是对于力矩、角动量等还是模模糊糊的,对于我来说,大多数经典力学问题就是“作用量+变分”,本题也不例外。为了让题目的实验意义更加明确,不妨将题目改成:
一根中性的均匀杆,它的一个端点带有一个点电荷,那么它(仅仅)在一个均匀电场中的运动是怎样的?
在这里,我们进一步简化,只考虑平面问题。杆属于刚体,为了描述杆的运动,我们需要描述杆上一点的运动,以及杆绕这一点的转动,也就是说,即使只考虑平面的情况,该系统也是有三个自由度的。设杆的带电荷那一端点的坐标为$(x,y)$,为了描述杆的转动,以这一端点为中心建立极坐标系,设杆的极角为$\theta$。设电势的函数为$U(x,y)$,因为只有一点带电(受力),因此势能是简单的。
在上一篇文章中,我们已经得到了电偶极子的等势面和电场线方程,这应该可以让我们对电偶极子的力场情况有个大致的了解了。当然,我们还是希望能够求出在这样的一个受力情况下,一个带电粒子是如何运动的。简单起见,在下面的探讨中,我们假定带电粒子的质量和电荷量均为1,至于电荷的正负,可以通过改变在$U=-\frac{k \cos\theta}{r^2}$中的k值的正负来控制。我们使用的工具依旧是理论力学中的欧拉-拉格朗日方程。
也许不少读者始终对公式感到头疼,更不用说是博大精深的理论力学了。但是请相信我,如果你花一点点心思去弄懂用变分法研究力学(或其他物理系统,但我目前只会用于力学)的基本思路和步骤,那么对你的物理研究是大有裨益的。因为在我眼中,学习了一丁点的理论力学知识后,我看到的只有物理的简洁与和谐。有兴趣的朋友可以看看我的那几篇《自然极值》等相关文章。
首先写出动能的表达式:$T=\frac{1}{2} (\dot{r}^2+r^2 \dot{\theta}^2)$
还有势能:$U=-\frac{k \cos\theta}{r^2}$
设想两个带有等量异号电荷的点电荷,它们之间的距离足够小,这样的一个模型被称为电偶极子(electric dipole)。我们研究电偶极子,主要是研究它在力学方面的性质。很多东西都可以用电偶极子来近似描述,比如一个小磁体周围的磁场,还有地球本身也可以近似看做一个偶极子来描述它的磁力情况,以及一些双原子分子的模型也被可以看做一个电偶极子模型,等等。在电偶极子模型中,两电荷的距离足够小,以至于我们忽略了一些关于距离的高次方项,只保留了线性部分,但对于物理探索来说,它已经足够精确,更重要的是,它足够简单,以至于我们可以容易把它清晰地描述出来。
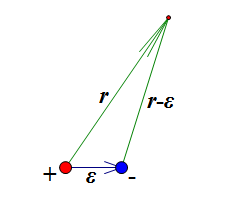
我们先来研究电偶极子产生的电势。设它们各自的电荷量为q和-q,两者距离为ε,根据库仑定律,一个点电荷产生的电势,正比于该电荷的电荷量,同时反比于到该点电荷的距离。那么,一个电偶极子产生的电势为
$U=C(\frac{q}{r}+\frac{-q}{|\vec{r}-\vec{\varepsilon}|})$————(1)
《科学》:我们发现了磁单极子
By 苏剑林 | 2009-10-02 | 33566位读者 | 引用电与磁具有很多相似性,那么,自然界允许只带有单一电荷的电子存在,那允不允许只有一个磁极的物体存在呢?也许会有的,英国物理学家保罗·狄拉克(Paul Dirac)早在1931年利用数学公式预言了这种物质的存在,并且把它叫做“磁单极子”。而今天,我们已经发现了它们的足迹! 磁单极子是理论物理学弦理论中指一些仅带有北极或南极单一磁极的磁性物质,它们的磁感线分布类似于点电荷的电场线分布。这种物质的存在性在科学界時有纷争,截至2008年尚未发现这种物体。可以说是21世纪物理学界重要的研究主题之一。在2009年9月3日的《科学》杂志上刊载了一篇记录人类首次观测到磁单极子的论文。








最近评论