科学空间|Scientific Spaces

经过第一部分，我们已经较好地提取了图像的文本特征，下面进行文字定位. 主要过程分两步：1、邻近搜索，目的是圈出单行文字；2、文本切割，目的是将单行文本切割为单字.

邻近搜索

我们可以对提取的特征图进行连通区域搜索，得到的每个连通区域视为一个汉字. 这对于大多数汉字来说是适用，但是对于一些比较简单的汉字却不适用，比如“小”、“旦”、“八”、“元”这些字，由于不具有连通性，所以就被分拆开了，如图13. 因此，我们需要通过邻近搜索算法，来整合可能成字的区域，得到单行的文本区域.

图13 直接搜索连通区域，会把诸如“元”之类的字分拆开

邻近搜索的目的是进行膨胀，以把可能成字的区域“粘合”起来. 如果不进行搜索就膨胀，那么膨胀是各个方向同时进行的，这样有可能把上下行都粘合起来了. 因此，我们只允许区域向单一的一个方向膨胀. 我们正是要通过搜索邻近区域来确定膨胀方向(上、下、左、右)：

邻近搜索* 从一个连通区域出发，可以找到该连通区域的水平外切矩形，将连通区域扩展到整个矩形. 当该区域与最邻近区域的距离小于一定范围时，考虑这个矩形的膨胀，膨胀的方向是最邻近区域的所在方向.

既然涉及到了邻近，那么就需要有距离的概念. 下面给出一个比较合理的距离的定义.

距离

图14 两个示例区域

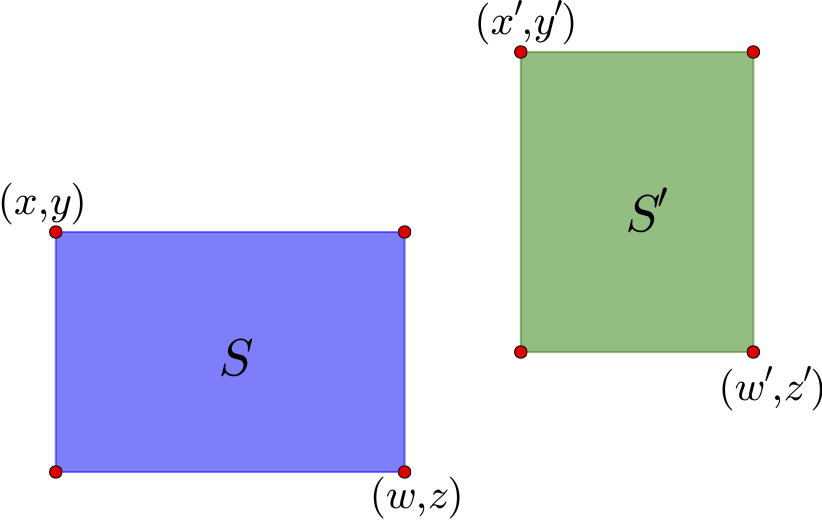
如上图，通过左上角坐标$(x,y)$和右下角坐标$(z,w)$就可以确定一个矩形区域，这里的坐标是以左上角为原点来算的. 这个区域的中心是$\left(\frac{x+w}{2},\frac{y+z}{2}\right)$. 对于图中的两个区域$S$和$S'$，可以计算它们的中心向量差
$$(x_c,y_c)=\left(\frac{x'+w'}{2}-\frac{x+w}{2},\frac{y'+z'}{2}-\frac{y+z}{2}\right)\tag{10}$$
如果直接使用$\sqrt{x_c^2+y_c^2}$作为距离是不合理的，因为这里的邻近应该是按边界来算，而不是中心点. 因此，需要减去区域的长度：
$$(x'_c,y'_c)=\left(x_c-\frac{w-x}{2}-\frac{w'-x'}{2},y_c-\frac{z-y}{2}-\frac{z'-y'}{2}\right)\tag{11}$$
距离定义为
$$d(S,S')=\sqrt{[\max(x'_c,0)]^2+[\max(y'_c,0)]^2}\tag{12}$$
至于方向，由$(x_c,y_c)$的幅角进行判断即可.

然而，按照前面的“邻近搜索*”方法，容易把上下两行文字粘合起来，因此，基于我们的横向排版假设，更好的方法是只允许横向膨胀：

邻近搜索 从一个连通区域出发，可以找到该连通区域的水平外切矩形，将连通区域扩展到整个矩形. 当该区域与最邻近区域的距离小于一定范围时，考虑这个矩形的膨胀，膨胀的方向是最邻近区域的所在方向，当且仅当所在方向是水平的，才执行膨胀操作.

结果

有了距离之后，我们就可以计算每两个连通区域之间的距离，然后找出最邻近的区域. 我们将每个区域向它最邻近的区域所在的方向扩大4分之一，这样邻近的区域就有可能融合为一个新的区域，从而把碎片整合.

实验表明，邻近搜索的思路能够有效地整合文字碎片，结果如图15.

图15 通过邻近搜索后，圈出的文字区域