在上一篇文章中,我们已经得到了电偶极子的等势面和电场线方程,这应该可以让我们对电偶极子的力场情况有个大致的了解了。当然,我们还是希望能够求出在这样的一个受力情况下,一个带电粒子是如何运动的。简单起见,在下面的探讨中,我们假定带电粒子的质量和电荷量均为1,至于电荷的正负,可以通过改变在$U=-\frac{k \cos\theta}{r^2}$中的k值的正负来控制。我们使用的工具依旧是理论力学中的欧拉-拉格朗日方程。
也许不少读者始终对公式感到头疼,更不用说是博大精深的理论力学了。但是请相信我,如果你花一点点心思去弄懂用变分法研究力学(或其他物理系统,但我目前只会用于力学)的基本思路和步骤,那么对你的物理研究是大有裨益的。因为在我眼中,学习了一丁点的理论力学知识后,我看到的只有物理的简洁与和谐。有兴趣的朋友可以看看我的那几篇《自然极值》等相关文章。
首先写出动能的表达式:$T=\frac{1}{2} (\dot{r}^2+r^2 \dot{\theta}^2)$
还有势能:$U=-\frac{k \cos\theta}{r^2}$
设想两个带有等量异号电荷的点电荷,它们之间的距离足够小,这样的一个模型被称为电偶极子(electric dipole)。我们研究电偶极子,主要是研究它在力学方面的性质。很多东西都可以用电偶极子来近似描述,比如一个小磁体周围的磁场,还有地球本身也可以近似看做一个偶极子来描述它的磁力情况,以及一些双原子分子的模型也被可以看做一个电偶极子模型,等等。在电偶极子模型中,两电荷的距离足够小,以至于我们忽略了一些关于距离的高次方项,只保留了线性部分,但对于物理探索来说,它已经足够精确,更重要的是,它足够简单,以至于我们可以容易把它清晰地描述出来。
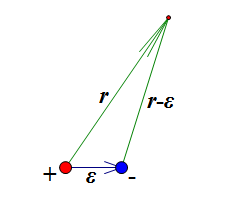
我们先来研究电偶极子产生的电势。设它们各自的电荷量为q和-q,两者距离为ε,根据库仑定律,一个点电荷产生的电势,正比于该电荷的电荷量,同时反比于到该点电荷的距离。那么,一个电偶极子产生的电势为
$U=C(\frac{q}{r}+\frac{-q}{|\vec{r}-\vec{\varepsilon}|})$————(1)








最近评论