科学空间|Scientific Spaces

在文章《生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼》中，我们为生成扩散模型DDPM构建了“拆楼-建楼”的通俗类比，并且借助该类比完整地推导了生成扩散模型DDPM的理论形式。在该文章中，我们还指出DDPM本质上已经不是传统的扩散模型了，它更多的是一个变分自编码器VAE，实际上DDPM的原论文中也是将它按照VAE的思路进行推导的。

所以，本文就从VAE的角度来重新介绍一版DDPM，同时分享一下自己的Keras实现代码和实践经验。

Github地址：https://github.com/bojone/Keras-DDPM

多步突破

在传统的VAE中，编码过程和生成过程都是一步到位的：
\begin{equation}\text{编码:}\,\,x\to z\,,\quad \text{生成:}\,\,z\to x\end{equation}

点击阅读全文...

拉格朗日

BoJone在之前的《自然极值》系列已经花了一定篇幅来讲述“极值”在自然界中是多么的普遍，它能够引导我们进行某些问题的思考，从而获得简单快捷的解答。接下来，我要说的一个更加令人惊讶的“事实”：“极值”不仅仅在某些数学或物理问题上给予我们创造性的思考，它甚至构建了整个经典力学乃至于整个物理学！这不是夸大其辞，这是物理学中被称为“最小作用量原理”的一个原理，很多物理学家（如费恩曼）被它深深吸引着，甚至认为它就是“上帝创造世界的终极公式”！（关于做小作用量原理，大家不妨看一下范翔所写的《最小作用量原理与物理之美》系列文章）

话说在18世纪，欧拉和拉格朗日开创了一条独特的道路，即用变分法来研究经典力学，从而使经典力学焕发出了新的活力，也由此衍生出了一个叫“理论力学”或“分析力学”的分支。用变分法研究力学有很多的好处，变分的对象一般都是标量函数，我们只需要写出动力系统的动能与势能表达式，就可以进行一系列的研究，比如列出质点的运动方程、判断平衡点的稳定性、求周期轨道等等（由于BoJone对理论力学研究还不够深入，无法举太多例子，但请相信，其作用远远不止这些），省去了不少繁琐的矢量性分析，这些都是在变分法发明前难以研究的。

点击阅读全文...

感谢Awank-Newton读者的来信，本文于2013.01.30作了修正，主要是弹性势能的正负号问题。之前连续犯了两个错误，导致得出了正确答案。现在已经修正。参考《平衡态公理的修正与思考》

在下面的两篇文章中，BoJone已经介绍了这个“旋转弹簧伸长”的问题，并从两个角度提供了两种解答方法。前者列出了一道积分方程，然后再转变为微分方程来解；后者直接从弹性力学的角度来列出一道二阶微分方程，两者殊途同归。
http://kexue.fm/archives/782/

http://kexue.fm/archives/826/

今天，再经过一段时间的变分法涉猎后，BoJone尝试从变分的角度（总能量最小）来给出一种新的解法。同样设r为旋转达到平衡后弹簧上一点到旋转中心的距离，该点的线密度为$\lambda =\lambda (r)$，该点到中心的弹簧质量为$m=m(r)$，旋转前的长度为$l_0$，旋转平衡后的长度为$l_1$。由于弹簧旋转后已经达到了平衡状态，由平衡态公理（参看《自然极值》系列），平衡意味着总能量“动能-势能”取极值。

点击阅读全文...

不可否认，变分法是非常有用而绝妙的一个数学工具，它“自动地”为我们在众多函数中选出了最优的一个，而免除了具体的分析过程。物理中的最小作用量原理则让变分法有了巨大的用武之地，并反过来也推动了变分法的发展。但是变分法的一个很明显的特点就是在大多数情况下计算相当复杂，甚至如果“蛮干”的话我们几乎连微分方程组都列不出来。因此，一些有用的技巧是很受欢迎的。本文就打算介绍这样的一个小技巧，来让某些变分问题得到一定的化简。

我是怎么得到这个技巧的呢？事实上，那是几个月前我在阅读《引力与时空》时，读到变分原理那一块时我怎么也读不懂，想不明白。明明我觉得是错误的东西，为什么可以得到正确的结果？我的数学直觉告诉我绝对是作者的错，可是我又想不出作者哪里错了，所以就一直把这个问题搁置着。最近我终于得到了自己比较满意的答案，并且窃认为是本文所要讲的这个技巧却被物理学家“误用”了。

技巧

首先来看通常我们是怎么处理变分问题的，以一元函数为例，对于求
$$S=\int L(x,\dot{x},t)dt$$

点击阅读全文...

ODE的坐标变换

熟悉理论力学的读者应该能够领略到变分法在变换坐标系中的作用。比如，如果要将下面的平面二体问题方程
$$\left\{\begin{aligned}\frac{d^2 x}{dt^t}=\frac{-\mu x}{(x^2+y^2)^{3/2}}\\
\frac{d^2 y}{dt^t}=\frac{-\mu y}{(x^2+y^2)^{3/2}}\end{aligned}\right.\tag{1}$$
变换到极坐标系下，如果直接代入计算，将会是一道十分繁琐的计算题。但是，我们知道，上述方程只不过是作用量
$$S=\int \left[\frac{1}{2}\left(\dot{x}^2+\dot{y}^2\right)+\frac{\mu}{\sqrt{x^2+y^2}}\right]dt\tag{2}$$
变分之后的拉格朗日方程，那么我们就可以直接对作用量进行坐标变换。而由于作用量一般只涉及到了一阶导数，因此作用量的变换一般来说比较简单。比如，很容易写出，$(2)$在极坐标下的形式为
$$S=\int \left[\frac{1}{2}\left(\dot{r}^2+r^2\dot{\theta}^2\right)+\frac{\mu}{r}\right]dt\tag{3}$$
对$(3)$进行变分，得到的拉格朗日方程为
$$\left\{\begin{aligned}&\ddot{r}=r\dot{\theta}^2-\frac{\mu}{r^2}\\
&\frac{d}{dt}\left(r^2\dot{\theta}\right)=0\end{aligned}\right.\tag{4}$$
就这样完成了坐标系的变换。如果想直接代入$(1)$暴力计算，那么请参考《方程与宇宙》:二体问题的来来去去(一)

点击阅读全文...

如果一直关注科学空间的朋友会发现，笔者一直对极值原理有偏爱。比如，之前曾经写过一系列《自然极值》的文章，介绍一些极值问题和变分法；在物理学中，笔者偏爱最小作用量原理的形式；在数据挖掘中，笔者也因此对基于最大熵原理的最大熵模型有浓厚的兴趣；最近，在做《量子力学与路径积分》的习题中，笔者也对第十一章所说的变分原理产生了很大的兴趣。

对于一样新东西，笔者的学习方法是以一个尽可能简单的例子搞清楚它的原理和思想，然后再逐步复杂化，这样子我就不至于迷失了。对于变分原理，它是估算路径积分的一个很强大的方法，路径积分是泛函积分，或者说，无穷维积分，那么很自然想到，对于有限维的积分估计，比如最简单的一维积分，有没有类似的估算原理呢？事实上是有的，它并不复杂，弄懂它有助于了解变分原理的核心思想。很遗憾，我并没有找到已有的资料描述这个简化版的原理，可能跟我找的资料比较少有关。

从高斯型积分出发

变分原理本质上是Jensen不等式的应用。我们从下述积分出发
$$\begin{equation}\label{jifen}I(\epsilon)=\int_{-\infty}^{\infty}e^{-x^2-\epsilon x^4}dx\end{equation}$$

点击阅读全文...

事实上，在论文《Dynamic Routing Between Capsules》发布不久后，一篇新的Capsule论文《Matrix Capsules with EM Routing》就已经匿名公开了（在ICLR 2018的匿名评审中），而如今作者已经公开，他们是Geoffrey Hinton, Sara Sabour, Nicholas Frosst。不出大家意料，作者果然有Hinton。

大家都知道，像Hinton这些“鼻祖级”的人物，发表出来的结果一般都是比较“重磅”的。那么，这篇新论文有什么特色呢？

在笔者的思考过程中，文章《Understanding Matrix capsules with EM Routing 》给了我颇多启示，知乎上各位大神的相关讨论也加速了我的阅读，在此表示感谢。

论文摘要

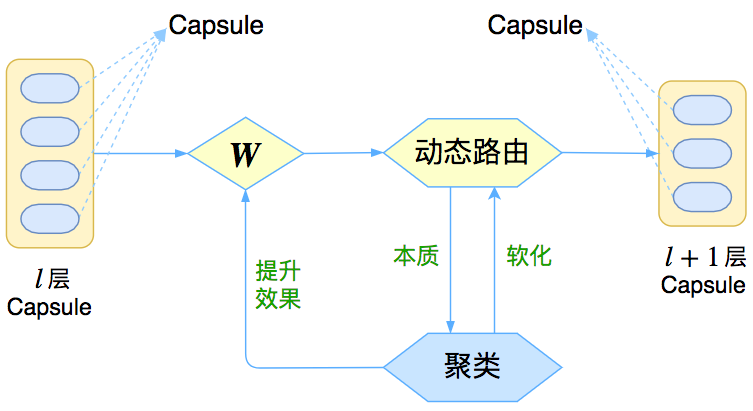
让我们先来回忆一下上一篇介绍《再来一顿贺岁宴：从K-Means到Capsule》中的那个图

Capsule框架的简明示意图

这个图表明，Capsule事实上描述了一个建模的框架，这个框架中的东西很多都是可以自定义的，最明显的是聚类算法，可以说“有多少种聚类算法就有多少种动态路由”。那么这次Hinton修改了什么呢？总的来说，这篇新论文有以下几点新东西：

1、原来用向量来表示一个Capsule，现在用矩阵来表示；

2、聚类算法换成了GMM（高斯混合模型）；

3、在实验部分，实现了Capsule版的卷积。

点击阅读全文...

最近在思考NLP的无监督学习和概率图相关的一些内容，于是重新把一些参数估计方法理了一遍。在深度学习中，参数估计是最基本的步骤之一了，也就是我们所说的模型训练过程。为了训练模型就得有个损失函数，而如果没有系统学习过概率论的读者，能想到的最自然的损失函数估计是平均平方误差，它也就是对应于我们所说的欧式距离。而理论上来讲，概率模型的最佳搭配应该是“交叉熵”函数，它来源于概率论中的最大似然函数。

最大似然

合理的存在

何为最大似然？哲学上有句话叫做“存在就是合理的”，最大似然的意思是“存在就是最合理的”。具体来说，如果事件$X$的概率分布为$p(X)$，如果一次观测中具体观测到的值分别为$X_1,X_2,\dots,X_n$，并假设它们是相互独立，那么
$$\mathcal{P} = \prod_{i=1}^n p(X_i)\tag{1}$$
是最大的。如果$p(X)$是一个带有参数$\theta$的概率分布式$p_{\theta}(X)$，那么我们应当想办法选择$\theta$，使得$\mathcal{L}$最大化，即
$$\theta = \mathop{\text{argmax}}_{\theta} \mathcal{P}(\theta) = \mathop{\text{argmax}}_{\theta}\prod_{i=1}^n p_{\theta}(X_i)\tag{2}$$

点击阅读全文...