科学空间|Scientific Spaces

universe_mystery_expand

1929年哈勃(Edwin Hubble)对河外星系的视向速度与距离的关系进行了研究。当时只有46个河外星系的视向速度可以利用，而其中仅有24个有推算出的距离，哈勃得出了视向速度与距离之间大致的线性正比关系。

不少宇宙学的书籍中都提到了标题，那么，为什么哈勃定律是宇宙各向同性的体现？或者说为什么宇宙各向同性就必然导致哈勃定律？

首先我们得需要了解一下宇宙学原理，它告诉我们宇宙在大尺度范围是均匀的、各向同性的。基于这个原理，我们会得到一些很奇怪的东西，如宇宙中的每一点都是宇宙的中心。另外，我们还可以得到：宇宙的（整体）运动情况在每一个方向都应该取相同的形式。

点击阅读全文...

开发太空天梯

漫话
BoJone认为，科学的意义并非在于无休止地计算，而是利用有限的科学理论来解释尽可能多的自然、生活现象。正因如此，科学家们追求和谐、简洁、优美的科学理论。科学就是想方设法地把未知变成已知，并在此基础上进一步发展。

随着媒体技术的发展，我们接触信息的渠道越来越多。每每我们从互联网或报纸上看到一则科学新闻时，我们几乎都会为之兴奋。但是，外行看热闹，内行看门道。对于真正热爱科学的朋友来说，也许会更加感兴趣新闻内容的来由。也就是说，我们希望进一步了解结论是怎样得出来的——哪怕只是在很浅的层面上认识。

点击阅读全文...

上星期，BoJone凭借简陋的物理知识，发表了《太阳帆技术的粗浅分析》一文，并转到了牧夫天文论坛上，希冀能够抛砖引玉。很幸运得到了牧夫上的高手的指正。他们指出了我的文章中$a=a_{ray}-a_G > 0$这一条件过于苛刻。因为，除了太阳光压外，还有另外一种力量能够战胜太阳引力——惯性离心力。

重新把上篇文章的一个结果列出来：
$$a=a_{ray}-a_G=(\frac{L}{2\pi c (\rho h+{m'}/S)}-GM_{sun})\frac{1}{r^2} $$

点击阅读全文...

相对于其他月份，2月的天空总显得有些寂寞。不过，这并不影响我们开心的情绪。因为通常中国最重要的节日——春节都发生在二月，今年也不例外。春节是农历年的开始，对中国人来说，它才是真正的2011的第一天！新年伊始，科学空间大家天天快乐，心想事成，愿BoJone的人生之旅上能够一直与各位科学爱好者相伴。

天象大观：

01日 金星距太阳: 45.4° W
05日 00:49 火星合日
08日 半人马α流星雨极大
12日 05:32 月合昴宿星团: 1.5° N
17日 17:15 海王星合日
22日 09:02 月合角宿一: 2.8° N
25日 13:26 月合心宿二: 2.9° S
25日 16:27 水星上合日.

点击阅读全文...

平面圆形限制性三体问题运动方程及能量积分
plane circular restricted three-body problem
02.04有重要修正！！

寒假一个很大的目标就是能够在三体问题的周期轨道上有点突破，于是就出动了“向量”、“复分析”、“微分方程”等理论“核武”，遗憾的是，“有心栽花花不开”，到今天还是没有多少进展。不过俗语也说“无心插柳柳成荫”，也不错。今天回看《天体力学引论》中的“圆形限制性三体问题”，经过一番思考，利用这些天的思考方法重新推导出了其运动方程和能量积分，也算是“意外收获”在此作为春节礼物与大家分享。

平面圆形限制性三体问题

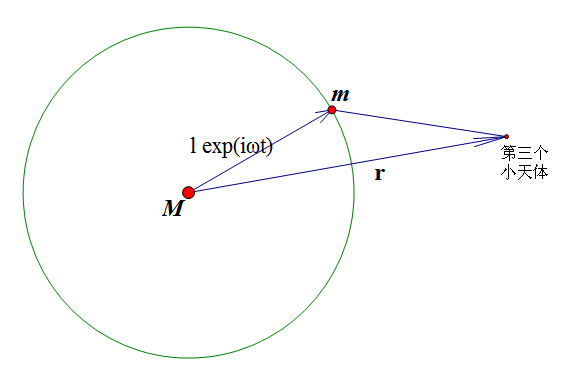
所谓“圆形限制性三体问题”，就是指两个大质量天体（质点）在它们相互引力作用下做圆周运动，假设第三天体（质量趋于0）只受到这两个天体的引力作用而不影响两个天体运行的一种运动情况。由于普通三体问题无法积分，而这个“限制性模型”能够把问题化简不少（不过还是不能积分出来的），因此也得到了一定应用。它的应用条件是：第三体质量小（如当前航天器与地球、太阳）、短程。注意短程也是相当重要的条件之一，注意短程也是相当重要的条件之一，质量越小应用范围越大。要是质量大的话，就不能计算太长的路程。

点击阅读全文...

大马国油双峰塔

这些日子来，BoJone迷上了两个东西：最小作用量和对称。这两个“东西”在物理学中几乎占据着最重要的地位，前边已经说过，通过最小作用量原理能够构建起当代整个物理学的框架，体现着自然界的“经济头脑”；后者则是守恒的体现，也对应着自然界的“美感”。本文主要是从最简单的层面谈谈对称。

对称的东西很重要，很美。当然，这里所指的是数学上的对称。数学上有很多问题都可以列出对称的式子，而且由于其对称性，因此求解过程一般比不对称的式子简单不少。据说，当代最前沿的物理学框架都是用群论描述的（包括广义相对论），而群论正是用来研究对称的有力工具，可见，对称和对称的方法在实际中有着广泛的应用。（当然本文不讨论群论，关键是BoJone也不懂群论...^_^）

我们先来看二次方程，根据韦达定理，二次方程都可以表达成下面的形式：
$$\begin{aligned}x_1+x_2=a \\ x_1 x_2=b\end{aligned}$$

这是一个多对称的形式！这里的对称体现在将$x_1,x_2$互相替换后方程形式依然不变。如果我们设$x_1=y_1+y_2,x_2=y_1-y_2$，就可以变成
$$2y_1=a,y_1^2-y_2^2=b$$

这样很快就求出$y_1,y_2$了，继而能够求出方程的两个根。

点击阅读全文...

在农村，7月是忙碌的月份，农民们要忙着收割稻谷，收割完后要晒谷，同时还得准备“下秧”，准备新一轮的耕，BoJone家自然也不例外。不过我家田比较少（1亩左右），收割机几分钟搞定，谷也三两天就晒完了。不过在晒谷的时候，BoJone在考虑一个“收谷”问题：

晒谷时得先把成堆的谷子摊开，薄薄地平铺在平地上，等到傍晚或即将下雨时（这是最惨的情况，搞不好会淋谷）就将其收起来。问题就源于这里，一般来说我们会把谷均匀地铺成矩形，要把所有的谷都推到矩形里或外的哪一点上，才使得我们做功做小？

这个问题还可以推广开来，例如对于一地任意形状的谷子（如三角形），把它集中堆到哪个点最“轻松”？一堆固定质量的谷子，要把它平铺成什么形状，才使得收谷时最“轻松”？当然，这个问题的解不仅仅用于“收谷”，在很多规划建设中也可以应用到，例如要在一个人口大致均匀的城市中建设一个服务中心，这个服务中心应该建在哪里？这有点类似于我们之前讨论过的费马点问题 ，都是费马点只考虑了三个点的距离，而这个问题得考虑所有点的距离。

点击阅读全文...

这是一个古老而有趣的问题，但在引入这个问题之前，我们首先来看一个简单的问题：

整数边直角三角形的面积能否为一个完全平方数？

答案是不能。我们可以举一些例子来检验一下，例如边长为3,4,5的直角三角形面积为6，6不是一个平方数；再如边长为5,12,13的直角三角形面积为30，30也不是一个平方数...当然，数学的最近目的是要求严格证明，而不是简单举例，否则就只得称为不完全归纳，这样得出来的是一个猜想，而不是“定理”，就好象著名的“哥德巴赫猜想”...本文我们将试图证明这个命题。

我们稍后还会发现，这个问题和以下问题是等价的：
是否存在一个面积为1的三边长都是有理数的直角三角形？

更让人意外的是，这个问题也等价于方程$x^4+y^4=z^4$并没有整数解，换句话说，我们要证明n=4时的“费马大定理”！

点击阅读全文...