| 【上一页】【下一页】【返回目录】 |
| §2-5 牛顿第二定律的积分形式——动能定理 |
| 1. 功(work) |
|
质点在力F的作用下,发生一无限小的位移dr ,F对质点所做的功定义为力和质点的位移的标积: |
|
 |
 |
|
如果质点沿路径L从1到2,则力对质点做功为: |
|
 |
|
冲量是力对时间的积累效应;而功是力对空间的积累效应。 |
| 注意: |
| 1、功是过程量,与路径有关。 |
| 2、功是标量,但有正负。 |
| 3、合力的功为各分力的功的代数和。 |
| |
| 2. 功率(power) |
|
力在单位时间内所作的功,称为功率。用P表示。 |
|
 |
| 在国际单位中: |
| 力的单位是牛顿(N); |
| 功的单位是N·m,叫焦耳; |
功率的单位是J/s,叫瓦(W)。 |
| |
| 例1:滑雪运动员的质量为m,沿雪道从A到B下滑高度为h,忽略摩擦力。求这一过程合力作的功。 |
|
【解】任一位置的合力为 |
 |
|
 |
|
因而合外力作功: |
|
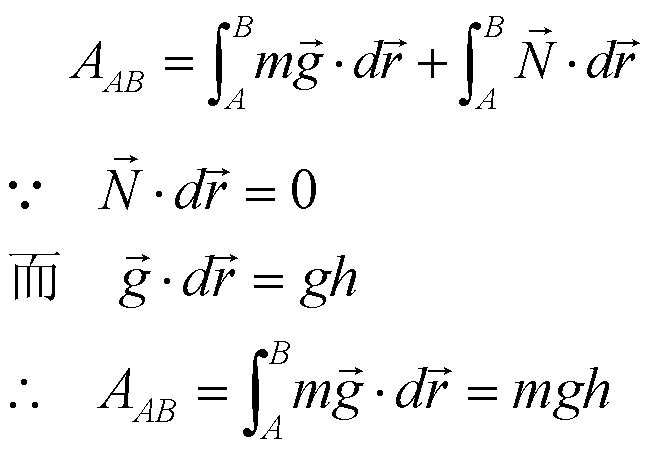 |
| |
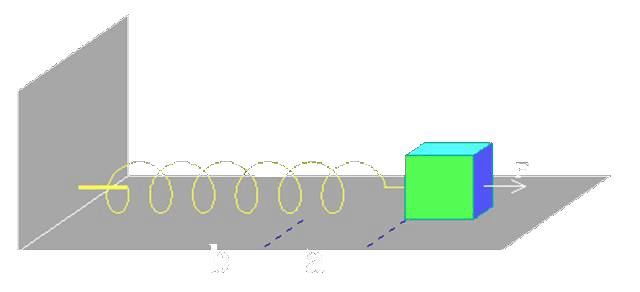
| 例2:水平放置的弹簧,一端固定,另一端系一物体。弹簧的劲度系数为k,求物体从a到b所作的功。 |
|
【解】任一位置物体受的弹力为 |
 |
|
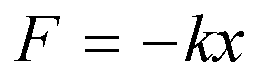 |
|
因而从a到b,弹力作功: |
|
 |
| |
| 3. 动能定理(kinetic
energy theorem) |
|
功既然是力的空间积累,将产生什么效果呢? |
 |
|
如图质点沿路径L从1到2作功为: |
|
 |
| 讨论: |
| ⅰ力对物体作功能改变质点的运动。 |
| ⅱ
在数量上和功对应的是mv2/2的量的改变,称之为动能。用Ek表示。 |
|
A12=Ek2-Ek1 |
| ——动能定理(合外力对质点作功等于质点动能的增量) |
| 例:质量为m的小球系在线的一端,另一端固定。线长l,小球由水平静止时下落,
求θ时的速度。 |
|
【解】合力作功为 |
|
|
 |
|
由动能定理,且v0=0,得: |
 |
|
 |
| |
|
|
![]()




![]()
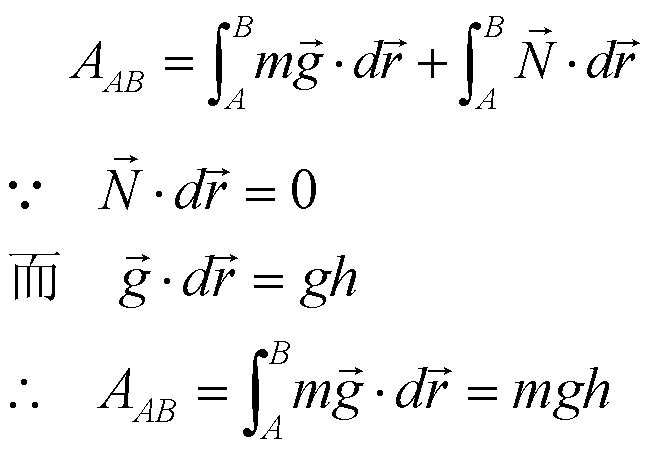

![]()





