第三章 运动的守恒定律
(Laws of conservation of Motion)
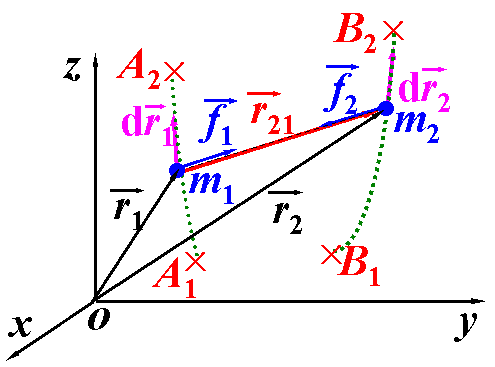

ⅲ°在无相对位移或相对位移与一对力垂直的情况下,一对力的功必为零。
例如:


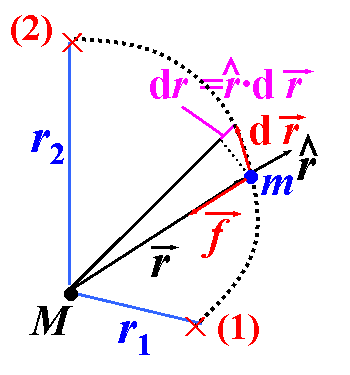
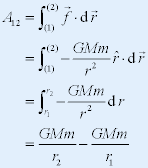





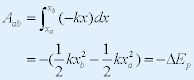



第三章 运动的守恒定律 |
(Laws of conservation of Motion) |
| 本章将研究对象由质点转向质点系统,重点研究系统的过程问题. |
| 一般地说,对于物体系统内发生的各种过程,如果某物理量始终保持不变,该物理量就叫做守恒量. |
| 本章将着重讨论能量守恒、动量守恒和角动量守恒.由宏观现象总结出的这几个守恒定律在微观世界已经过严格 |
| 检验,证明它们同样有效.守恒定律是自然规律最深刻、最简洁的陈述,它比物理学中其它定律(例如牛顿运动定律 |
| )更重要、更基本. |
| §3.1 保守力 成对力作功 势能 |
| 1. 一对力的功 |
| 根据牛顿第三定律,力总是成对出现的,有作用力就有反作用力。称为一对力。 |
| 同一系统中出现的一对力称为内力,下面讨论系统中质点m1和m2之间的内力作功。 |
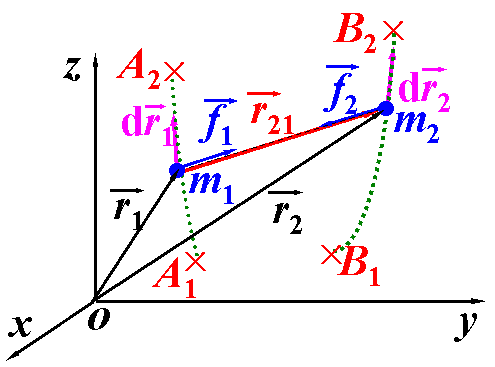 |
 |
| 说明: |
| ⅰ° 两质点间的“一对力”所做功之和等于其中一个质点受的力沿着该质点相对另一质点所移动的路径所做的功。 |
| ⅱ° A与参考系选取无关。 |
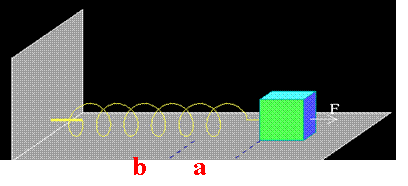
ⅲ°在无相对位移或相对位移与一对力垂直的情况下,一对力的功必为零。 |
例如: |
| |
| |
 |
 |
| (图二) |
| 2. 保守力(conservative force) |
| 成对力中,有一种特殊情况:如果一对力的功与相对移动的路径无关,而只决定于相互作用物体的始末相对位置,这样的力称为 |
| 保守力。 |
| 例:M和m两质点的引力作功。如图三。 |
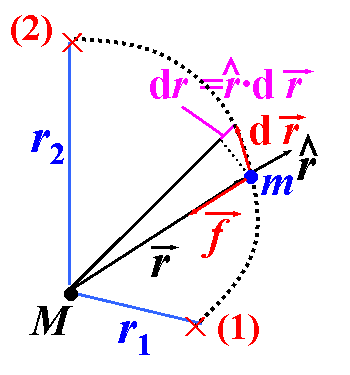 |
| (图三) |
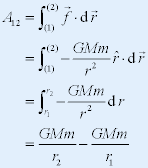 |
| 特殊地,(1)与(2)重合,则 |
| 因此,保守力有另一特征:一质点相对于另一质点沿闭合路径移动一周时,它们之间的保守力作功为零。 |
| |
| |
 |
| (图四) |
| 许多力都是保守力,如:引力、静电力、弹簧弹力等等。 |
| 作功与路径有关的力称为非保守力。 |
| 例如: |
| ▲ 摩擦力(耗散力): 一对滑动摩擦力作功恒为负; |
| ▲ 爆炸力:作功为正。 |
| 3. 势能(potential energy) |
| 利用保守力的功与路径无关的特点,可引入“势能” 的概念,以简化作功的计算。 |
| ⅰ° 势能:由物体之间的相互作用和相对位置决定的能量。以Ep表示,也叫位能。 |
| ⅱ° 系统由位形(1)变到位形(2)的过程中,保守力做的功相应于其势能的改变的负值。 |
| |
| ⅲ° 势能是相对的,应先选择好势能零点。若规定系统在位形(0)的势能为零, 则: |
| |
| ⅳ° 势能属于相互作用的系统;势能不依赖于参考系的选择,不要将势能零点的选择与参考系的选择相混淆。 |
| ⅴ° 引力势能(取无穷远为零势点) |
 |
 |
| (图五) |
| ⅵ° 重力势能(取地面为零势点) |
 |
 |
| (图六) |
| ⅵ° 弹性势能(取弹簧自然长度为零势点) |
| 在弹簧零点附近,任一位置的弹力为: |
| |
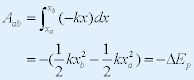 |
  |
| (图七) (图八) |
| 可见,弹性力是保守力。 |
| |
| 4. 势能和保守力的关系 |
| 势能的定义: |
| |
 |
| (图九) |
| 所以有: |
| |
| 若势能为EP(x,y,z),则有: |
 |
| —— EP 的梯度(gradient) |
| |