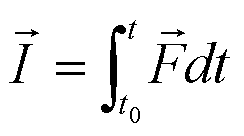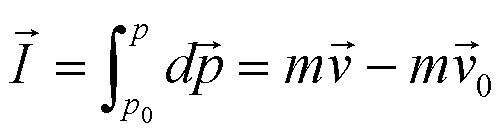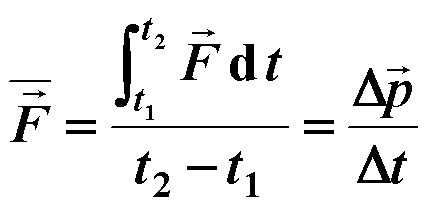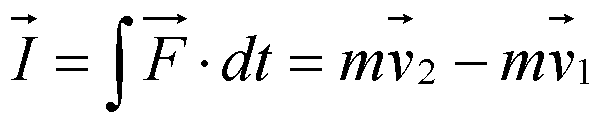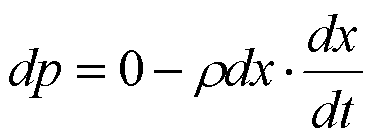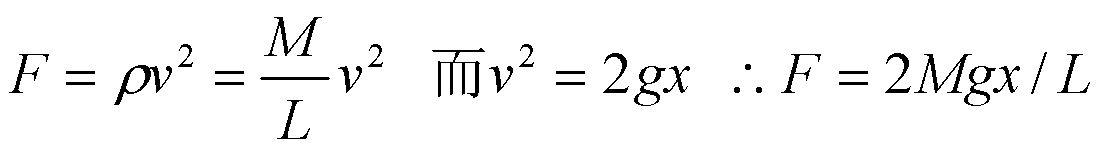| 【上一页】【下一页】【返回目录】 |
| §2-4 牛顿第二定律的积分形式——动量定理 |
| 前面讨论的牛顿定律的微分形式: |
|
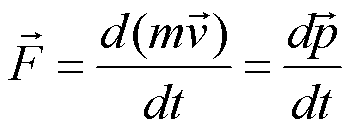 |
| 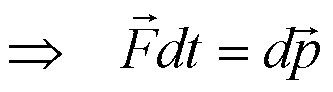 |
| ⅰ
式中Fdt表示力在时间dt内的积累量,叫dt时间内质点所受合外力的冲量(impulse),用dI
表示。 |
|
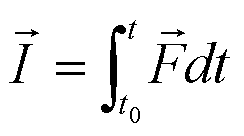 |
| ⅱ
由上式得: |
| 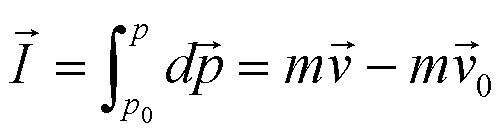 |
|
在运动过程中,作用于质点上的合力在一段时间内的冲量等于质点动量的增量,这就是动量定理。 |
| ⅲ
动量定理与牛顿第二定律一样,都反映了质点运动状态的变化与力的作用关系。但牛顿第 |
 |
| 二定律是瞬时规律;动量定理则是力对质点作用的积累效果。 |
| ⅳ
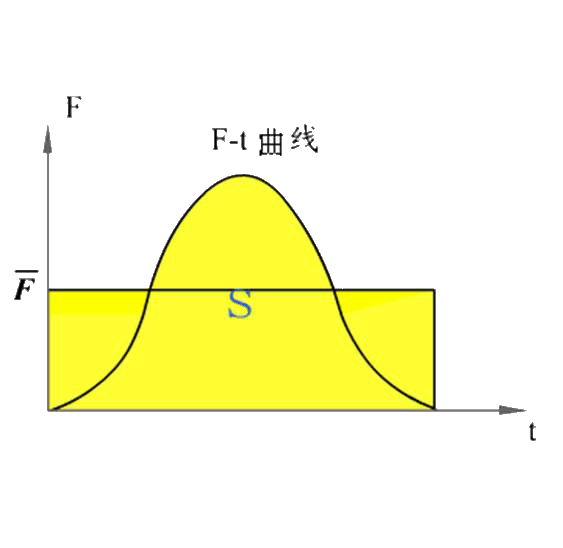
动量定理在处理碰撞和冲击问题时很方便,这时的作用力往往是快速变化的,如图。称为冲力。 |
|
数学上精确给出冲力与时间的关系往往是困难的,这时可以通过实验定出平均冲力: |
| 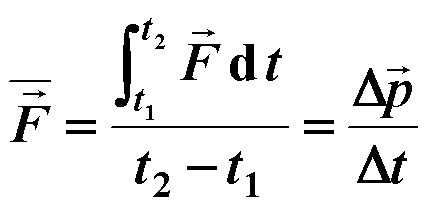 |
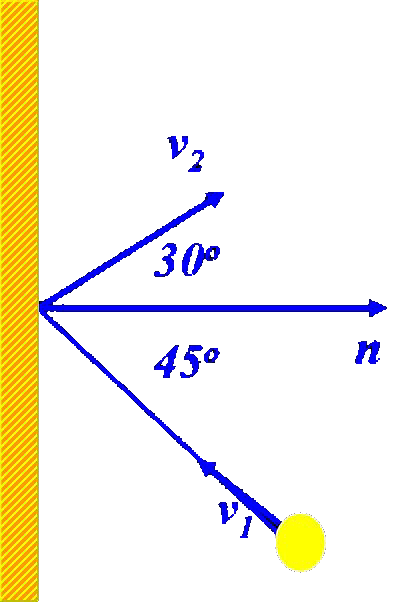
| 例1:质量为2.5g的乒乓球以10m/s的速率飞来,被板推挡后,又以20m/s的速率飞出。设两速度在垂直于板面的同一平面内,且 |
它们与板面法线的夹角分别为45度和30度,求:(1)乒乓球得到的冲量;(2)若撞击时间为0.01s,求板施于球的平均冲力 |
| 的大小和方向。 |
| 【解】取挡板和球为研究对象,由于作用时间很短,忽略重力影响。设挡板对球的冲力为,则有: |
| 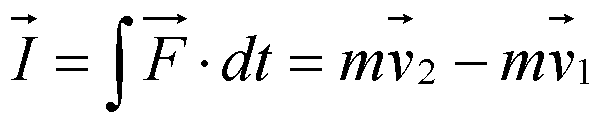 |
| 取坐标系,将上式投影,有: |
 |

|
|
α为I与x轴的夹角
。 |
| |
 |
| 此题也可用矢量法解,作矢量图用余弦定理和正弦定理,可得: |
|
|
| |
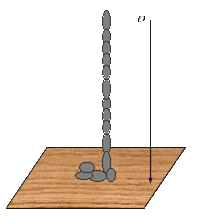
| 例2:一质量均匀分布的柔软细绳铅直地悬挂着,绳的下端刚好触到水平桌面上,如果把绳的上端放开,绳将落在桌面上。试证明:在
|
| 绳下落的过程中,任意时刻作用于桌面的压力,等于已落到桌面上的绳重量的三倍。 |
| 【证明】设t时刻已有x长的柔绳落至桌面,随后的dt时间内将有质量为pdx=Mdx/L的柔绳以
的速率dx/dt碰到桌面 |
| 而停止,它的动量变化为: |
| 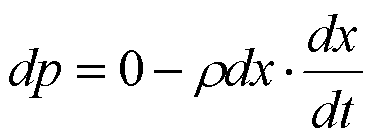 |
 |
| 一维运动可用标量 |
| 根据动量定理,桌面对柔绳的冲力为: |
|
 |
| 柔绳对桌面的冲力:F
= -F',即 |
|
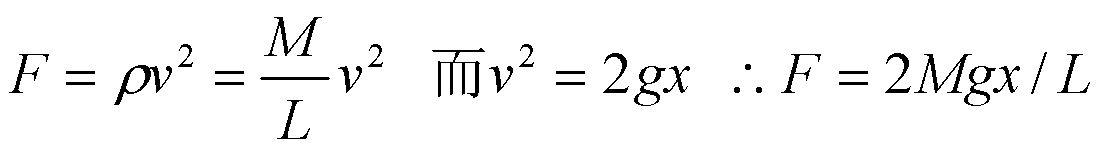 |
| 而已落到桌面上的柔绳的重量为mg=Mgx/L |
| 所以 |
|
F总=F+mg=2Mgx/L+Mgx/L=3Mg |
| |
|
|
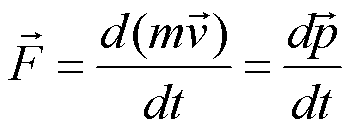
![]()