| 【上一页】【下一页】【返回目录】 | |
| §4-3 刚体定轴转动的角动量守恒定律 | |
| 1. 刚体对转轴的角动量 | |
|
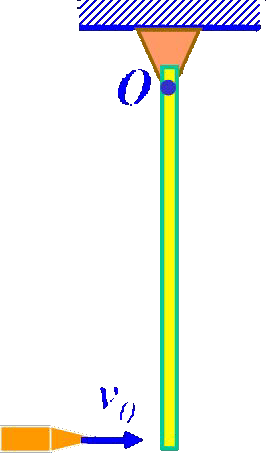
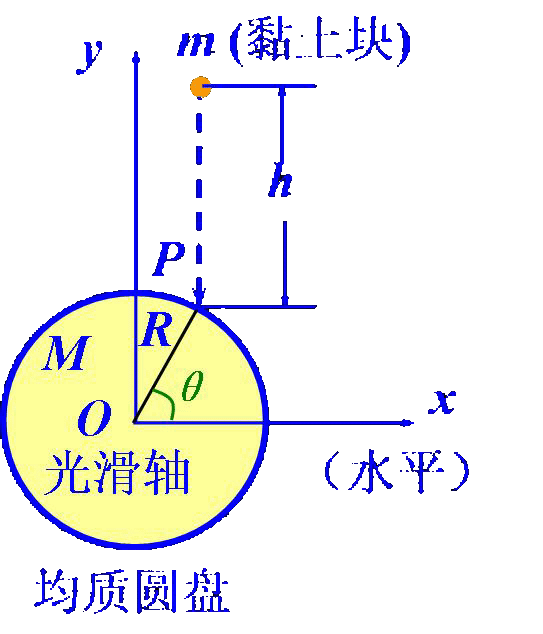
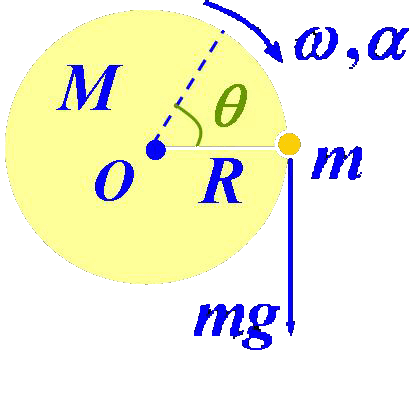
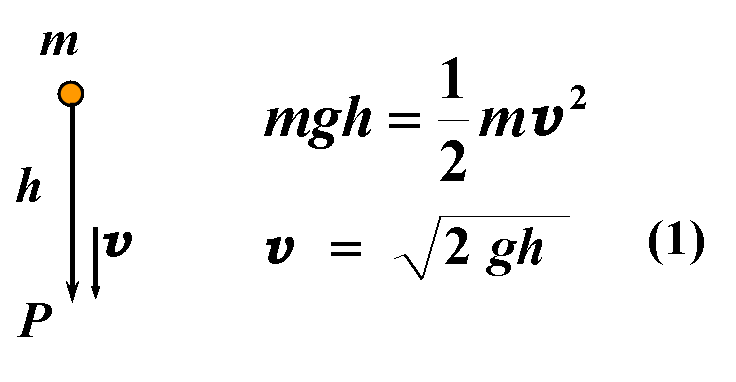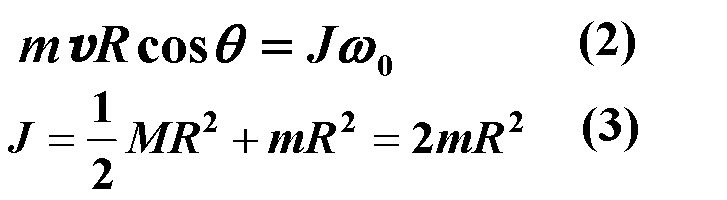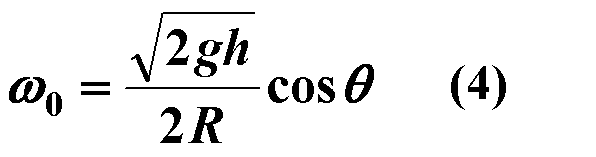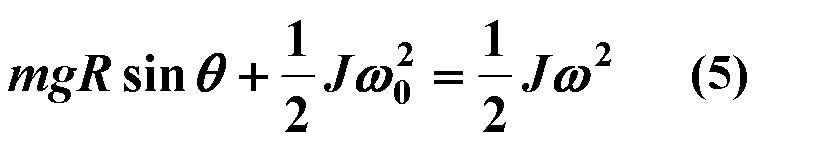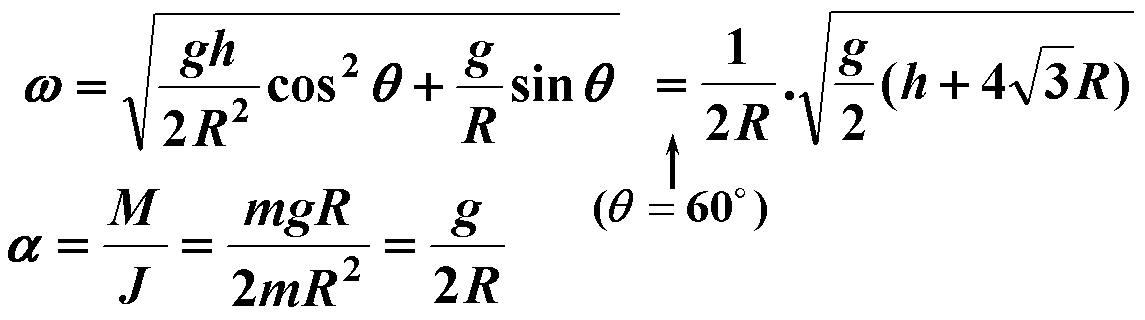质点对固定点的角动量为： |
 |
|
|
|
|
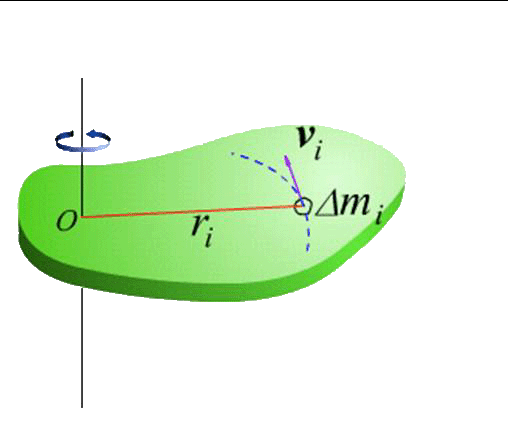
刚体定轴转动时，其上的任意一个质元均有r⊥v。因此，其角动量为： |
|
|
|
|
|
刚体总的角动量为： |
|
|
|
|
|
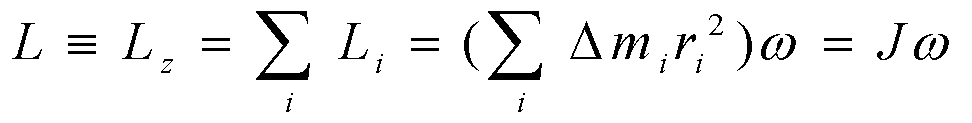
刚体对固定转动轴的角动量L，等于它对该轴的转动惯量J 和角速度ω的乘积。 |
|
| 2. 刚体对转轴的角动量定理 | |
|
根据力矩的定义，在定轴转动中，可用标量表示： |
|
|
|
|
|
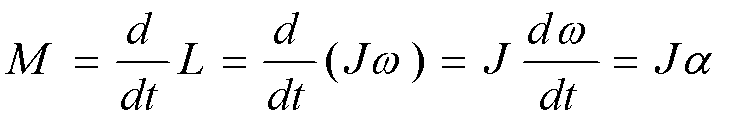
其积分形式： |
|
|
|
|
|
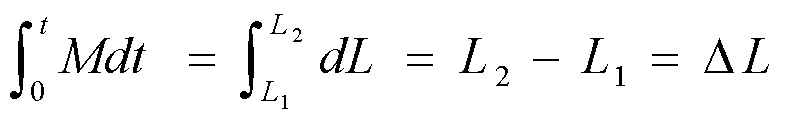
这就是刚体对转轴的角动量定理。左边为对某个固定轴的外力矩的作用在某段时间内的积累效果，称为冲量矩。 |
|
|
当J不变时
|
|
|
当J也改变时
|
|
| 3. 刚体对转轴的角动量守恒定律 | |
|
在刚体的角动量定理中，特殊地： |
|
|
若M=0，则L=常量 |
|
|
就是说，如果对某一固定转轴，刚体所受的合外力矩为零，则此刚体对该固定轴的角动量分量保持不变。——刚体角动量守恒定律 |
|
| 例1：一质量为m的子弹以水平速度射入一静止悬于顶端长棒的下端，求子弹和棒共同运动的角速度ω。已知棒长为l，质量为M. | |
| 【解】这是完全非弹性碰撞，系统相对O点的角动量守恒： |
 |
|
|
|
| 例2：如图示，已知：h，R，M=2m，θ=60度。求：碰撞后的瞬刻盘ω0=？P转到x轴时盘ω=？α=？ | |
| 【解】M下落 |
 |
|
|
|
| 对（m +盘）系统，碰撞中重力对O 轴力矩可忽略，系统角动量守恒： | |
|
|
|
| 由(1)(2)(3)得： |
 |
|
|
|
| 对（m + M +地球）系统，只有重力作功，机械能守恒。令P、x 重合时 EP = 0，则： | |
|
|
|
| 由(3)(4)(5)得： | |
|
|
|
