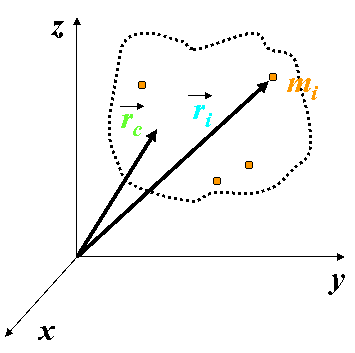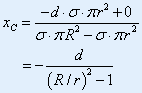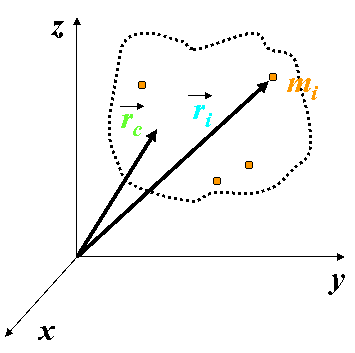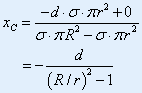| 【上一页】【下一页】【返回目录】 |
| |
| §3.4 质心运动定理 动量守恒定律 |
| ( theorem of motion of center of mass
law of conservation of momentum ) |
| 1. 质心(center of mass) |
| 考虑由一刚性轻杆相连的两质点组成的系统(如下面的flash1),当我们将它斜向抛出时,它在空间的运动很复杂,每个质点都不是 |
| 抛物线轨迹,但两质点连线上某点C却作抛物线的运动,C点的运动规律就象质量全部集中在C点,全部外力也象作用在C点一样。这个特殊 |
| 点C就是质点系统的质心。 |
|
|
| (flash1,请点击解说按钮) |
质心就是质点系的质量中心,设一个质点系 N个质点,质量: 位矢: 位矢: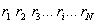 |
定义质心 C 的位矢为: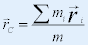 (m为总质量) (m为总质量) |
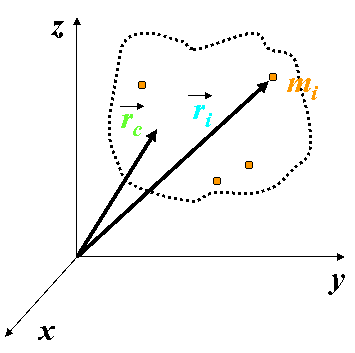 |
| (图一) |
| 质心位矢在直角坐标系中的分量式为: |
 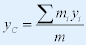 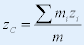 |
| 如果质量分布是连续的 ,则求和化为积分: |
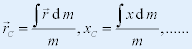 |
| ⅲ°具有对称性,且质量分布均匀的物体,质心在对称中心。 |
| ⅳ°对于不太大的实物,质心与重心重合。 |
| 例1:求半圆形铁丝的质心。已知半径为R。 |
解:如图却坐标系,由对称性,质心一定在y轴上。设线密度为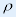 ,则 ,则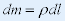 |
由定义: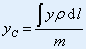 |
由图: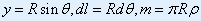 则: 则: |
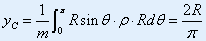 |
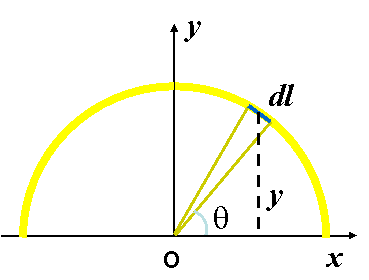 |
| (图二) |
| 例2:如图三示,求挖掉小圆盘后系统的质心坐标。 |
 |
| (图三) |
| 解:由对称性分析,质心C应在x轴上。 |
令 为质量的面密度,则质心坐标为: 为质量的面密度,则质心坐标为: |
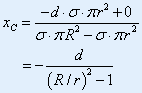 |
| 2. 质心运动定理 |
| 质心的运动速度为: |
 |
| 总动量: |
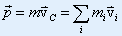 |
| 由: |
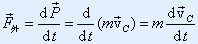 |
| 得: |
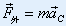 |
| —-质心运动定理 |
| 质心的运动如同一个质点。该质点质量等于整个质点系的质量,而此质点所受的力是质点系的所有外力之和。 |
| 在质点系的质心运动定理中,若质点系所受的外力的矢量和为零,即: |
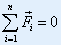 |
| 则有: |
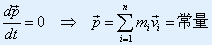 |
| 质点系所受合外力为零时,质点系的总动量不随时间改变。这就是质点系的动量守恒定律。 |
| v它是一个普适规律,只要合外力为零,就满足。 |
| v注意总动量的矢量性。 |
| v具有分量形式。也就是说,动量守恒可在某一方向上成立,条件是这个方向的合外力为零。 |
| v对于应用动量定理时,只要求作用力的合力为零,而不必知道系统内部相互作用的细节。 |
| 例:半径为R的1/4圆弧,质量为M,置于光滑平面上。其上质量为m的物体自顶由静止滑下,求m到底时,M在水平方向的移动 |
| 量。 |
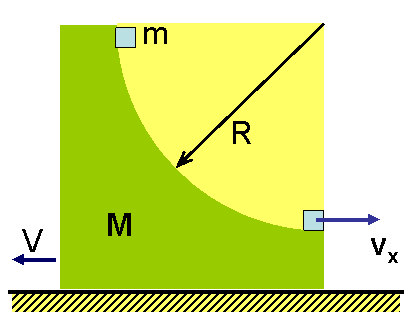 |
| (图四) |
| 解: |
| 系统水平方向动量守恒,则任一时间有: |
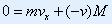 |
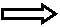 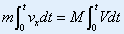 |
 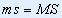 |
又因为: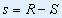 ,则上式: ,则上式: |
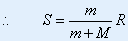 |
| |
|