混沌的世界——“星之轨迹”的研究
By 苏剑林 | 2012-01-13 | 41193位读者 | 引用(本文已被刊登在2012年1月的《天文爱好者》上,于笔者而言这是一份很棒的新年礼物!)
在去年第七期《天爱》上,我们看到了N体问题所呈现出来的一些对称、漂亮的周期轨道,这体现了N体问题和谐有序的一面。但是这仅仅是N体问题的冰山一角,笔者也提到过N体问题的本质是混沌、无序的,通俗来讲就是非常乱,无法用数学方程来精确描述。这看起来是一种不完美。但试想,探索当初伽利略将望远镜对准月球后,看到的是如想象中光滑的月面,那么他还会惊叹宇宙的神奇吗?
本文就让我们来更深入地了解一下N体问题的研究历史。
观测&拟合时代
由于人类的自我优越感以及日月星辰东升西落的经验,让我们长期都认为地球是宇宙的中心。第一个比较系统提出地心说的人当属天文学家欧多克斯(Eudoxus,死于公元前347年左右),但他的地心说是非常粗糙的,以至于无法解释很多基本现象,如无法准确预言日食和解释行星逆行等。但亚里士多德接受了地心说,并且由于他在政治和科学上的权威,使地心说免去了夭折的命运。后来托勒密通过他的本轮,完善了地心说,使之延续到了16世纪。
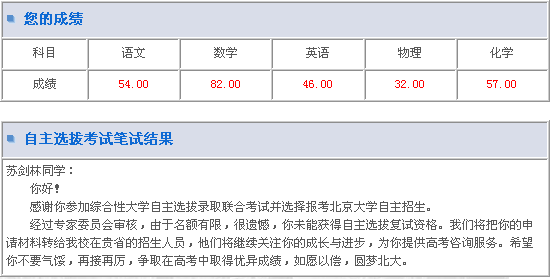
我的自主招生成绩公布了
By 苏剑林 | 2012-03-04 | 41670位读者 | 引用引力透镜——用经典力学推导光的偏转公式
By 苏剑林 | 2012-04-30 | 66759位读者 | 引用引力透镜
————用经典力学推导光的引力偏转角公式
在2012年第四期的《天文爱好者》上,Richard de Grijs(何锐思)教授的《引力透镜——再领科学潮》一文详细而精彩地讲述了有关引力透镜方面的知识,尤其是它在天文方面的重要应用,让我收获颇丰。笔者在赞叹作者优美的文笔和译者程思浩同好的生动翻译之余,也感到了一丝不足。文章主要讲了引力透镜在天文研究中所扮演的重要角色,却未对引力透镜的原理、本质方面多加描述。时空的扭曲是广义相对论给出的答案,可是难道仅仅从经典力学就不能领略丝毫?藉此,BoJone这在里对引力透镜多说些东西,与大家相互学习研究。当然,由于我只是一个初出茅庐的业余爱好者,其中的不当之处还望各位斧正。
相对论、对称和第四维
By 苏剑林 | 2012-05-01 | 85459位读者 | 引用这篇文章其实在年初就完成了。
众所周知,我们生活在一个平坦的世界中。正如我们能够感受到的那样,在这个被称为“欧几里得平直空间”的世界里,空间里两点间的最短曲线是两点间的直线段,空间里的任意直角三角形都满足勾股定理,每个物体都有着自己的长、宽、高,它们都随着时间的流逝而运动着。这种世界观把时间独立于空间之外,作为一个独特的研究对象。但是自爱因斯坦在1905年发表狭义相对论以来,我们的宇宙就被描述成为了由三维空间和一维时间组成的“四维时空”,在这里,时间和空间的地位是等价的。不少同好们也许会感到非常困惑:即使证明了时间与空间的确存在着某种联系,也不必要把时间描述成是世界的一维吧?在我们的感官里,时间明明就和空间的三维差别甚大,时间和空间怎么能够等同起来呢?其实答案很简单:为了美。把时间看成与空间等价的一维之后,整个力学体系体现出一种前所未有的对称美,这种美不仅让人赏心悦目,而且极大地方便了我们进一步处理问题。
对称
诡异的Dirac函数
By 苏剑林 | 2013-01-14 | 48392位读者 | 引用量子力学中有一个很诡异的函数——Dirac函数,它似乎在物理的不少领域都有很大作用,它也具有明显的物理意义,但认真地看它却又感觉它根本就不是函数!这个“似而非是”的东西究竟是什么呢?让我们从一个物理问题引入:
设想一条质量为1,长度为$2l$的均匀直线,很显然直线的密度为$\rho=\frac{1}{2l}$;将直线的中点放置于坐标轴的原点,我们就有
$$\rho(x)=\left\{ \begin{array}{c}\frac{1}{2l} (-l \leq x \leq l)\\0 (x < -l , x > l)\end{array}\right.$$
所以有
$$\int_{-\infty}^{+\infty} \rho(x)dx=1$$
今天傍晚看到了彩虹!当然这算不上什么奇观,但还是一道美丽的风景。
人说“不经历风雨,怎么见彩虹”,我发现彩虹不一定是在雨后的,今天我看彩虹的时候,就是暴风雨前夕。彩虹是在18点10分左右出现的,持续了5分钟左右吧,看着看着,雨越下越大,我被迫停止欣赏了,不过彩虹也随之消失了。
用一个老相机简单记录了一下这道亮丽的风景!这是我第一次拍摄彩虹^_^
不知道是相机问题还是真有其事,在照片上发现有两条彩虹。难道这次的彩虹是”双彩虹“?那可真是奇观了!

很老的家用数码相机,没有广角,不能拍摄全景,这是用photoshop把两张图片拼凑起来的,效果不好
“未解之谜”:为何不讲中点矩形法则?
By 苏剑林 | 2012-07-20 | 57971位读者 | 引用前言
在之前的一些文章中,我们已经指出过现行教材的一些毛病。比如主次不当(最明显的是那些一上来就讲线性方程组的线性代数教程)、缺乏直观性、缺少引导性等,我想其中最主要的原因可能是过于随大流了,别人怎么编我们也跟着怎么编,缺乏自己的观点和逻辑,因此导致一些常见的毛病就一直流传了下来。也许正因如此,就导致了有那么一种奇怪的现象——明明有一种计算量少的、精确度高一些的方法,教科书几乎从未提及;另外一种计算量稍大、精确度稍低的方法,但每一本同类教科书都讲述了它。不能不说这是一个“未解之谜”......
本文要讲的就是这样的两种方法,它们分别是用来求定积分近似值的“中点矩形法则”和“梯形法则”。对于后者我想绝大多数学习过微积分的朋友都会有印象,它就是那个几乎出现在了所有微积分教材的方法;而前者我相信不少读者都未曾听闻,但让人意外的是,它的计算量稍低,精确度却稍高。本文就简单介绍这两种方法,并且比较它们的精度。而本文的独特之处在于,证明过程沿用了《复分析:可视化方法》的思路,使用几何方法漂亮地估计误差!
我们的目标是在难以精确计算的情况下,通过一定的方法求出$\int_a^b f(x)dx$的近似值,这些方法基本上都是利用了积分即面积的思想。
两种不同的方法
折腾windows 8和ubuntu 12
By 苏剑林 | 2012-08-30 | 21910位读者 | 引用这是一篇用Windows 8完成的文章。
快开学了,华师2号就要报道了,所以就提前入手一台手提电脑,联想Z575AM-ASI,四千元的AMD,4核,64位机器。
我的台式机已经是六年前的产品了,联想的家悦系列,只有512MB内存。所以相比之下,这新机器配置还过得去吧,对于CPU,我个人还是倾向于AMD的,因为我的那台家悦台式也是AMD的CPU,所以对它很有好感。新兴的联想专卖店没有AMD手提,所以还得提前向他们预订。
Windows8
手提本身没有预装操作系统,专卖店很随手地为我装了一个win7,而且还只是ghost版本的,时不时会卡死,感觉很不好,刚好前些日子在网上开始发布Windows8了,所以就马上把Win7格掉,装上Windows8了。安装过程很顺利,由于还没有正式发布,所以还没有激活,这段时间纯粹体验中。等正式版发布了,再计划买一个正版光盘吧









最近评论