若有几列波同时在介质中传播,则它们各自将以原有的振幅、频率和波长独立传播;在几列波相遇处,质元的位移等于各列波单独
能分辨不同的声音正是这个原因;叠加原理的重要性在于可以将任一复杂的波分解为简谐波的组合。
当波强度过大时,如爆炸产生的冲击波,不满足线性方程,这时叠加原理不适用。
干涉现象-满足相干条件的两列波在空间任一点相遇时,在空间某些点处,振动始终加强,而在另一些点处,振动始终减弱或消失,

相干条件:
① 频率相同;
② 振动方向相同;
③ 有固定的相位差。
两列波干涉的一般规律留待在后面光的干涉中再去分析。下面研究一种特殊的、常见的干涉现象—— 驻波。
两列相干的行波沿相反方向传播而叠加时,就形成驻波,它是一种常见的重要干涉现象。
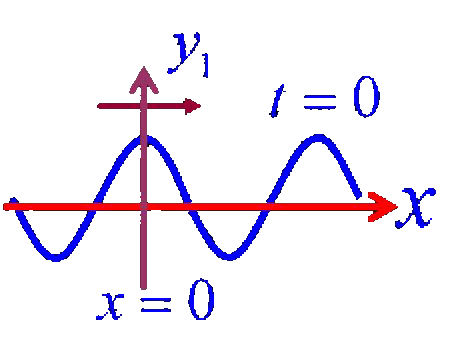

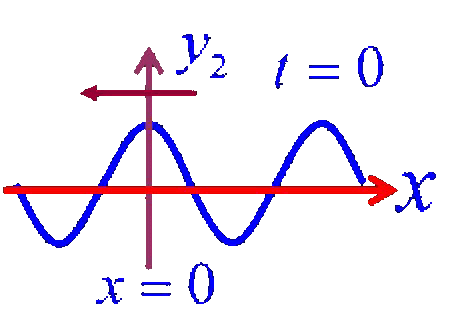
其合成波称为驻波其表达式:

利用三角函数关系求出驻波的表达式:

它表示各点都在作简谐振动,各点振动的频率相同,是原来波的频率。但各点振幅随位置的不同而不同。
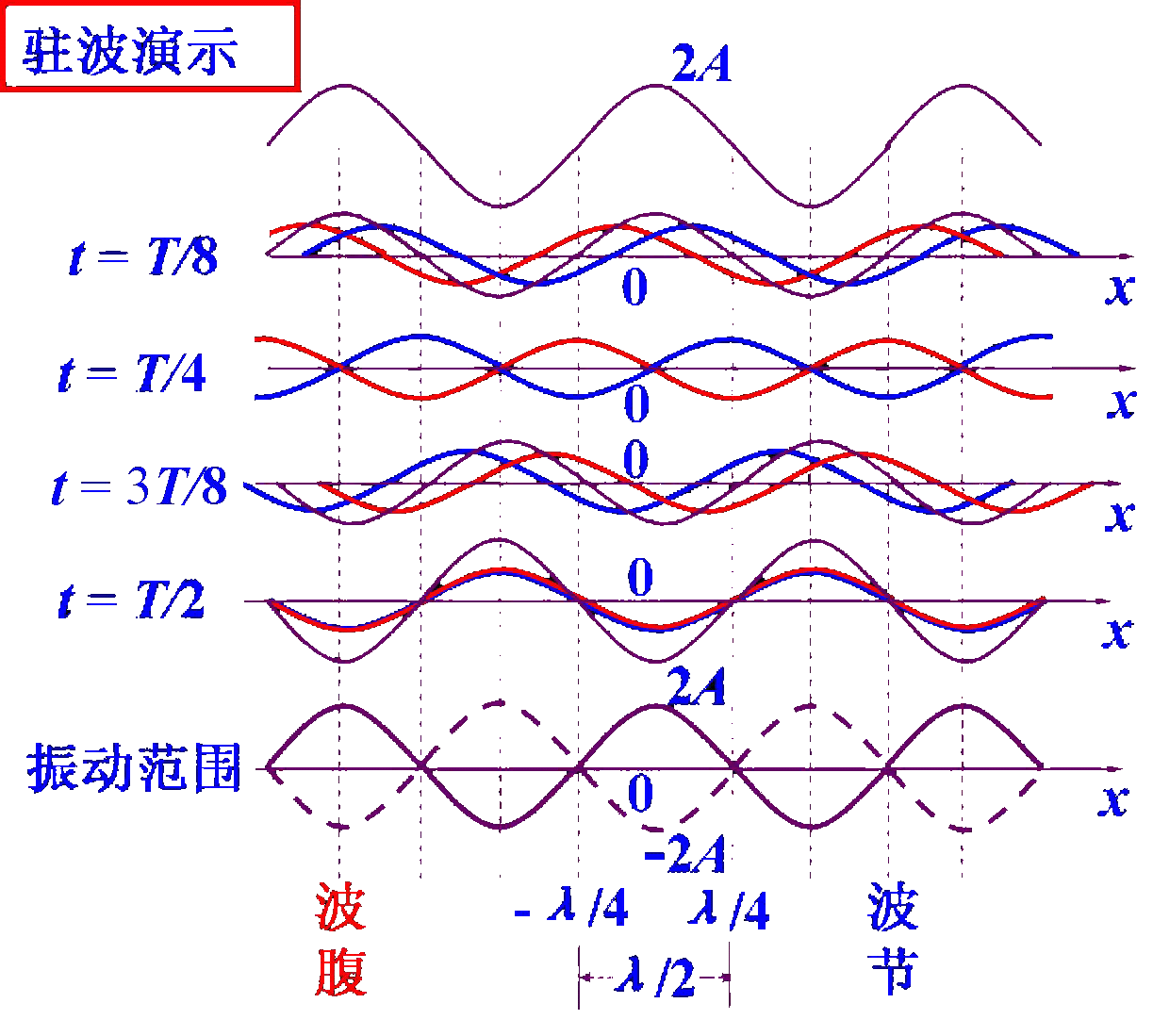


一维驻波
二维驻波
①振幅:
各处不等大,出现了波腹(振幅最大处)和波节(振幅最小处)。相邻波节间距λ/2,测波节间距可得行波波长。
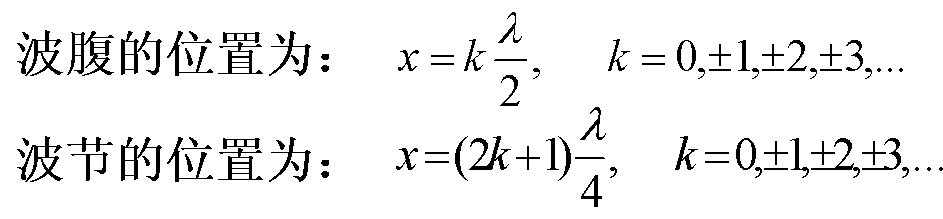
②相位:
相位中没有x 坐标,故没有了相位的传播。驻波是分段的振动。相邻段振动相位相反
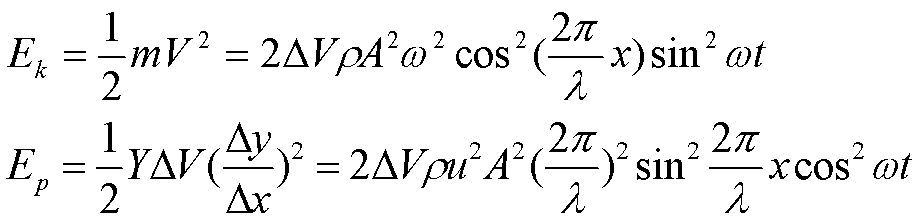
1. 在波节处相对形变最大,势能最大;在波腹处相对形变最小,势能最小。势能集中在波节。
2. 当各质点回到平衡位置时,全部势能为零;动能最大。动能集中在波腹。
3. 能量从波腹传到波节,又从波节传到波腹,往复循环,能量不被传播。它是媒质的一种特殊的运动状态,稳定态。