第六章 机械振动
为积分常数
是决定简谐运动状态的物理量,称为振动的相位, 
时，
时，
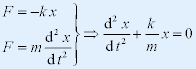
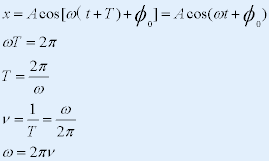
第六章 机械振动 |
| v物体在一定位置附近所作的来回往复的运动称为机械振动. |
| v广义地讲,任何一个物理量在某个定值附近反复变化,都可称为振动. |
| 下面的flash演示的是一些机械振动的例子（把鼠标放到闹钟和心脏上或点击齿轮的黑色螺杆或者开关均可查看效果） |
| （flash一） |
| 振动是自然界中最常见的一种物质运动形式。 |
| 共同特征：运动在时间、空间上的周期性 |
| 机械振动分类： |
| v按振动规律分：简谐、非简谐、随机振动 |
| v按产生振动原因分：自由、受迫、自激、参变振动 |
| v按自由度分：单自由度系统、多自由度系统振动 |
| v按振动位移分：角振动、线振动 |
| v按系统参数特征分：线性、非线性振动 |
| §6-1 简谐振动(Simple Harmonic Motion) |
| 物体运动时,如果离开平衡位置的位移(或角位移)按余弦(或正弦)的规律随时间变化，这种运动称为简谐振动。 |
| 简谐振动是理想化模型。 许多实际的小振幅振动，都可以看成简谐振动。 |
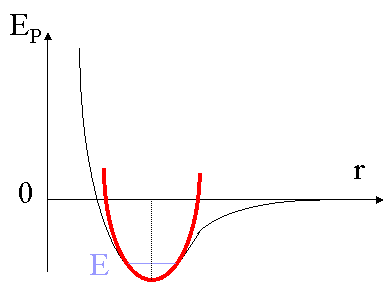
| 例. 双原子分子两个原子之间的振动(如图一) |
| |
| (图一) |
| 简谐振动是最简单最基本的振动，复杂的振动都可以分解为一些简谐振动的叠加。 |
| 1.简諧振动的特征极其表式 |
| 弹簧振子 |
| （flash二） |
| |
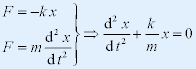| 令： |
| |
| |
| 求解得： |
| 为积分常数 |
| 物体作简谐振动时的速度与加速度 |
| |
| |
| （图二） |
| 2. 简谐振动的振幅,周期,频率和相位 |
| (1)振幅：简谐振动的物体离开平衡位置的最大位移的绝对值A |
| (2)周期和频率 ：完成一次完整振动所经厉的时间称为周期 |
| |
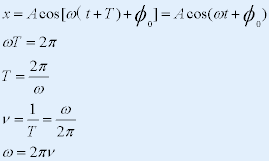| (3)相位和初相 |
| 是决定简谐运动状态的物理量,称为振动的相位, |
| t=0时相位,称为初相位,简称初相. |
| 3.简谐振动的矢量图示法 |
| flash三是矢量图示法的示意图。 |
| （flash三） |
| 沿半径 A 的圆周匀速运动的参数方程 |
| |
| 旋转矢量法优点： |
| v直观地表达谐振动的各特征量 |
| v便于解题,特别是确定初相 |
| v便于振动合成 |
| 旋转矢量A与谐振动的对应关系 |
| |
| ４.几钟常见的简諧振动 |
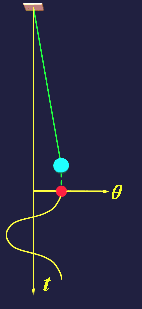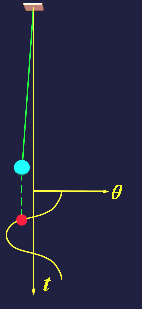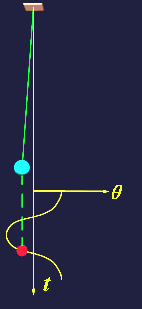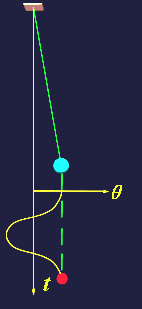
| （1）单摆 |
| |
| （图三、单摆的振动） |
| |
| 当时， |
| |
| 在角位移很小的时候，单摆的振动是简谐振动。角频率,振动的周期分别为： |
| |
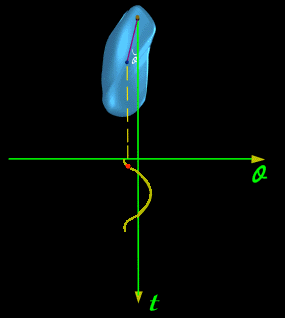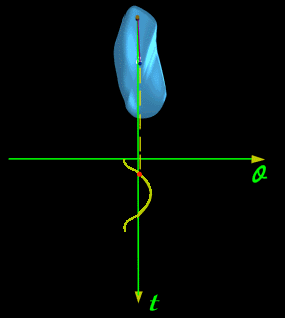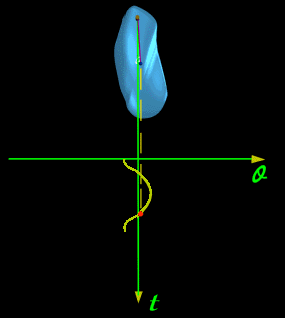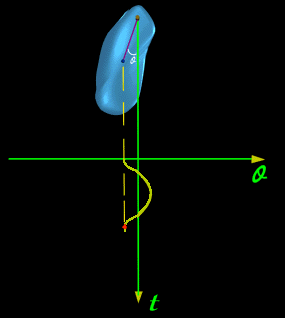
| （2）复摆 |
| |
| （图四、复摆的振动） |
| |
| 当时， |
| |
| 同样可得简谐振动参数： |
| |
| 振动的角频率、周期完全由振动系统本身来决定。 |
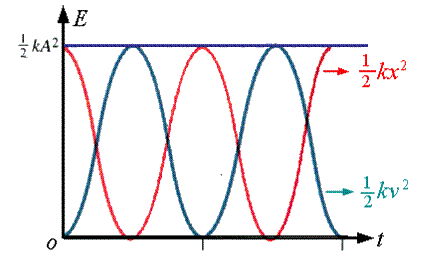
| 5.简谐振动的能量 |
| |
| |
| （图五、简谐振动的能量图） |
| 简谐振动的动能： |
| |
| 简谐振动的势能： |
| |
| 简谐振动的总能量： |
| |