昨天一个QQ好友让我帮忙解决一道物理题目：

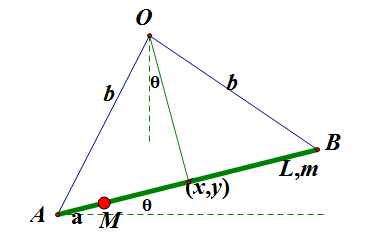
长为L的均匀木杆重Q，在木杆上离A端L/4处放有一重为Q/2的重物，平衡时，木杆AB与水平面的夹角θ有多大？

木杆平衡

木杆平衡

看上去挺有趣的。于是我先记了下来，今天早上思考了一会儿，得出了下面的结果。其中我解答并没有直接受力分析，而是用了我们之前已经谈到过的“最小势能原理”：平衡系统中的势能必取极（小）值。

首先如图所示，把问题一般化，记两个细绳长度为b，木杆程度为L，质量为m；木块质量为M，距离A点的距离为a。设中心点处的坐标为(x,y)，不难列出$x^2+y^2=b^2-(\frac{L}{2})^2=r^2$，于是可以设$y=r \cos\theta,x=r \sin\theta$（这里和一般的极坐标有点出入，但这只是为了计算方便），可见，变量只有θ，这是一个一自由度的问题。

选择O点所在的平面为参考平面，不难得出木杆的势能为$E_{p1}=-mgr \cos\theta$，而木块的势能为$E_{p2}=-Mgr[r \cos\theta+(\frac{L}{2}-a)\sin\theta]$，总势能为
$$E_p=-mgr \cos\theta-Mg[r \cos\theta+(\frac{L}{2}-a)\sin\theta]$$

对其求导并令导数为0，
$$\frac{dE_p}{d\theta}=mgr \sin\theta+Mg[r \sin\theta-(\frac{L}{2}-a)\cos\theta]=0$$

解得$tan\theta=\frac{M(L-2a)}{2r(M+m)}$
其中$r=\sqrt{b^2-(\frac{L}{2})^2}$

对于QQ好友原来提出的问题，得到：$tan\theta=\frac{\sqrt{3}}{18}$

可以从以下几个定性的角度来对答案进行检验：

1、检查左右两边的量纲是否相等。本答案两边都无量纲，显然满足；
2、当$a=\frac{L}{2}$时，显然不会倾向某一边，该答案满足；
3、当$a > \frac{L}{2}$时，显然会倾向另外一边，该答案满足（tanθ变负数）；
4、当M为0时，显然偏角为0；当M远远大于m时，偏角与M,m无关。该答案满足。
5、当b非常长（趋于无穷）时，显然偏角不会明显，于是θ趋于0。该答案也满足。

很多时候检验并不是要我们重新计算一遍，而是像上面一样找一些特例来验证。因为一个正确的答案必须能满足物理现象的各个方面。这些特例其实就描述了这个物理系统的性质。这是定性的方法。掌握一些定性方法，能让我们在全然不知具体细节的情况下，“摸清”答案具有的各种性质，甚至“猜出”答案！这正是诸多物理大师如费米、费恩曼、惠勒等擅长的。

转载到请包括本文地址：https://kexue.fm/archives/1536

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jan. 21, 2012). 《[问题解答]木杆平衡 》[Blog post]. Retrieved from https://kexue.fm/archives/1536

@online{kexuefm-1536,
        title={[问题解答]木杆平衡},
        author={苏剑林},
        year={2012},
        month={Jan},
        url={\url{https://kexue.fm/archives/1536}},
}