诡异的Dirac函数
By 苏剑林 | 2013-01-14 | 39636位读者 | 引用量子力学中有一个很诡异的函数——Dirac函数,它似乎在物理的不少领域都有很大作用,它也具有明显的物理意义,但认真地看它却又感觉它根本就不是函数!这个“似而非是”的东西究竟是什么呢?让我们从一个物理问题引入:
设想一条质量为1,长度为$2l$的均匀直线,很显然直线的密度为$\rho=\frac{1}{2l}$;将直线的中点放置于坐标轴的原点,我们就有
$$\rho(x)=\left\{ \begin{array}{c}\frac{1}{2l} (-l \leq x \leq l)\\0 (x < -l , x > l)\end{array}\right.$$
所以有
$$\int_{-\infty}^{+\infty} \rho(x)dx=1$$
“未解之谜”:为何不讲中点矩形法则?
By 苏剑林 | 2012-07-20 | 46105位读者 | 引用前言
在之前的一些文章中,我们已经指出过现行教材的一些毛病。比如主次不当(最明显的是那些一上来就讲线性方程组的线性代数教程)、缺乏直观性、缺少引导性等,我想其中最主要的原因可能是过于随大流了,别人怎么编我们也跟着怎么编,缺乏自己的观点和逻辑,因此导致一些常见的毛病就一直流传了下来。也许正因如此,就导致了有那么一种奇怪的现象——明明有一种计算量少的、精确度高一些的方法,教科书几乎从未提及;另外一种计算量稍大、精确度稍低的方法,但每一本同类教科书都讲述了它。不能不说这是一个“未解之谜”......
本文要讲的就是这样的两种方法,它们分别是用来求定积分近似值的“中点矩形法则”和“梯形法则”。对于后者我想绝大多数学习过微积分的朋友都会有印象,它就是那个几乎出现在了所有微积分教材的方法;而前者我相信不少读者都未曾听闻,但让人意外的是,它的计算量稍低,精确度却稍高。本文就简单介绍这两种方法,并且比较它们的精度。而本文的独特之处在于,证明过程沿用了《复分析:可视化方法》的思路,使用几何方法漂亮地估计误差!
我们的目标是在难以精确计算的情况下,通过一定的方法求出$\int_a^b f(x)dx$的近似值,这些方法基本上都是利用了积分即面积的思想。
两种不同的方法
费曼积分法——积分符号内取微分(4)
By 苏剑林 | 2012-06-26 | 62069位读者 | 引用趁着早上有空,就赶紧把这篇文章写好吧。下午高考成绩要公布了,公布后也许又会有一段时间忙碌了。这应该是“费曼积分法”系列最后一篇文章了。它主要讲的还是费曼积分法的一个实例。不同的是,这是BoJone首次独立地用费曼积分法解决了一个问题。之前提到的一些例子,都是书本提供并结合了提示,BoJone才把它们算出来的。所以这个问题有着点点纪念意义。
数学研发论坛上wayne曾求证这样的命题:
$\int_0^{\infty}\frac{f(x,2m-1)-\sin x}{x^{2m+1}}dx$其中,f(x,2m-1)表示sinx的2m-1阶泰勒展开
如m=1时,
$$\int_0^{\infty}\frac{x-\sin x}{x^3}dx$$
m=2时
$$\int_0^{\infty}\frac{x-\frac{x^3}{6}-\sin x}{x^5}dx$$
借助软件我发现结果是:
$\frac{\pi(-1)^{m-1}}{2(2m)!}$
费曼积分法——积分符号内取微分(3)
By 苏剑林 | 2012-06-23 | 45270位读者 | 引用由于自行车之旅的原因,这篇文章被搁置了一个星期,其实应该在一个星期前就把它写好的。这篇文章继续讲讲费曼积分法的一些例子。读者或许可以从这些不同类型的例子中,发现它应用的基本方向和方法,从而提升对它的认识。
例子2:
$$\int_0^{\infty} \frac{\sin x}{x}dx$$
这也是一种比较常见的类型,它的形式为$\int \frac{f(x)}{x}dx$,对于这种形式,我们的第一感觉就是将其改写成参数形式$\int \frac{f(ax)}{x}dx$,这样的目的很简单,就是把分母给消去了,与$\int \frac{x}{f(x)}dx$的求积思想是一致的。但是深入一点研究就会发现,纵使这样能够消去分母,使得第一次积分变得简单,但是到了第二次积分的时候,我们发现,它又会变回$\int \frac{f(x)}{x}dx$的积分,使我们不能继续进行下去,因此这个取参数的方法大多数情况下都是不行的。
费曼积分法——积分符号内取微分(2)
By 苏剑林 | 2012-06-12 | 81672位读者 | 引用上一篇文章我对“费曼积分法”做了一个简单的介绍,并通过举例来初步展示了它的操作步骤。但是,要了解一个方法,除了知道它能够干什么之外,还必须了解它的原理和方法,这样我们才能够更好地掌握它。因此,我们需要建立“积分符号内取微分”的一般理论,为进一步的应用奠基。
一般原理
我们记
$$G(a)=\int_{m(a)}^{n(a)} f(x,a)dx$$
在这里,f(x,a)是带有参数a的关于x的函数,而积分区间是关于参数a的两个函数,这样的积分也叫变限积分,可以理解为是普通定积分的推广。我们记F(x,a)为f(x,a)的原函数,也就是说$\frac{\partial F(x,a)}{\partial x}=f(x,a)$,那么按照微积分基本定理,我们就有:
$$G(a)=F(n(a),a)-F(m(a),a)$$
费曼积分法——积分符号内取微分(1)
By 苏剑林 | 2012-06-10 | 71042位读者 | 引用昨天在研究一个最优化问题时,遇到了一个这样的积分:
$$\int \frac{1}{\cos^3 \theta} d\theta$$
然后就顺便研究了一下这种类型的函数的积分。一般来讲,这类积分可以写成$\int cos^n \theta d\theta$或$\int sin^n \theta d\theta$,其中n是一个整数。
首先我们来解决n=1的情况,我们很容易就有$\int cos\theta d\theta=sin\theta +C$或$\int sin\theta d\theta=-cos\theta +C$,这是一个基本的结果。
如果n是大于1的正整数,那么可以用递推的方法来搞定:
[春礼]《方程与宇宙》:圆形限制性三体问题(七)
By 苏剑林 | 2011-02-04 | 20027位读者 | 引用平面圆形限制性三体问题运动方程及能量积分
plane circular restricted three-body problem
02.04有重要修正!!
寒假一个很大的目标就是能够在三体问题的周期轨道上有点突破,于是就出动了“向量”、“复分析”、“微分方程”等理论“核武”,遗憾的是,“有心栽花花不开”,到今天还是没有多少进展。不过俗语也说“无心插柳柳成荫”,也不错。今天回看《天体力学引论》中的“圆形限制性三体问题”,经过一番思考,利用这些天的思考方法重新推导出了其运动方程和能量积分,也算是“意外收获”在此作为春节礼物与大家分享。
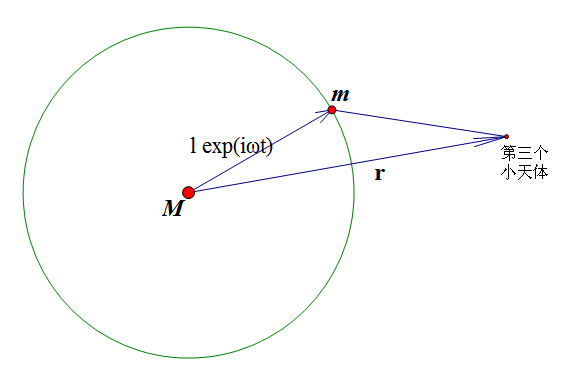
所谓“圆形限制性三体问题”,就是指两个大质量天体(质点)在它们相互引力作用下做圆周运动,假设第三天体(质量趋于0)只受到这两个天体的引力作用而不影响两个天体运行的一种运动情况。由于普通三体问题无法积分,而这个“限制性模型”能够把问题化简不少(不过还是不能积分出来的),因此也得到了一定应用。它的应用条件是:第三体质量小(如当前航天器与地球、太阳)、短程。注意短程也是相当重要的条件之一,注意短程也是相当重要的条件之一,质量越小应用范围越大。要是质量大的话,就不能计算太长的路程。









最近评论