30
Apr
引力透镜——用经典力学推导光的偏转公式
By 苏剑林 | 2012-04-30 | 62498位读者 | 引用引力透镜
————用经典力学推导光的引力偏转角公式
引力透镜效应造成的爱因斯坦十字
在2012年第四期的《天文爱好者》上，Richard de Grijs（何锐思）教授的《引力透镜——再领科学潮》一文详细而精彩地讲述了有关引力透镜方面的知识，尤其是它在天文方面的重要应用，让我收获颇丰。笔者在赞叹作者优美的文笔和译者程思浩同好的生动翻译之余，也感到了一丝不足。文章主要讲了引力透镜在天文研究中所扮演的重要角色，却未对引力透镜的原理、本质方面多加描述。时空的扭曲是广义相对论给出的答案，可是难道仅仅从经典力学就不能领略丝毫？藉此，BoJone这在里对引力透镜多说些东西，与大家相互学习研究。当然，由于我只是一个初出茅庐的业余爱好者，其中的不当之处还望各位斧正。
13
Jan
混沌的世界——“星之轨迹”的研究
By 苏剑林 | 2012-01-13 | 38647位读者 | 引用（本文已被刊登在2012年1月的《天文爱好者》上，于笔者而言这是一份很棒的新年礼物！）
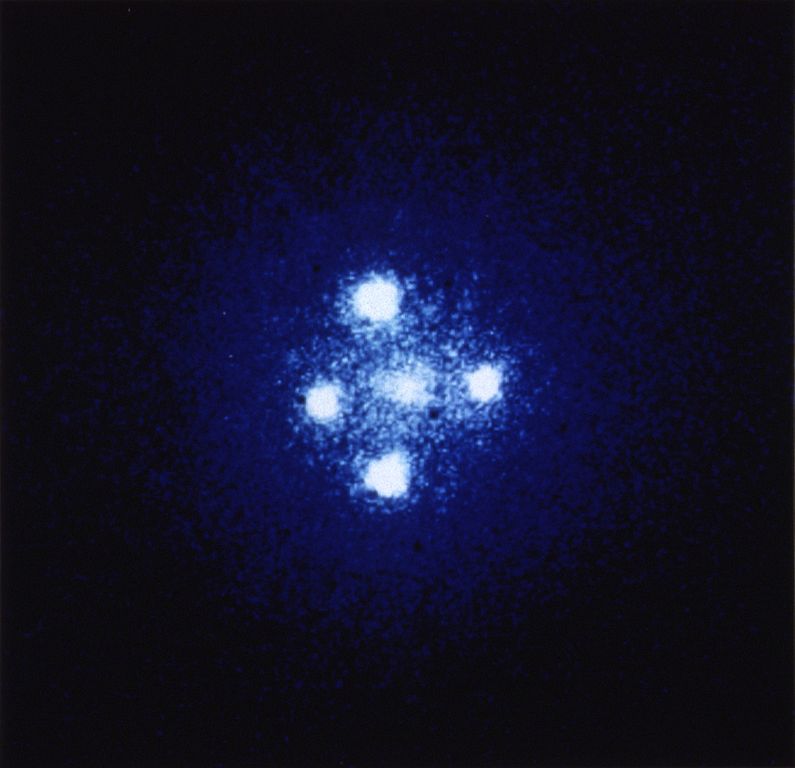
在去年第七期《天爱》上，我们看到了N体问题所呈现出来的一些对称、漂亮的周期轨道，这体现了N体问题和谐有序的一面。但是这仅仅是N体问题的冰山一角，笔者也提到过N体问题的本质是混沌、无序的，通俗来讲就是非常乱，无法用数学方程来精确描述。这看起来是一种不完美。但试想，探索当初伽利略将望远镜对准月球后，看到的是如想象中光滑的月面，那么他还会惊叹宇宙的神奇吗？
本文就让我们来更深入地了解一下N体问题的研究历史。
观测&拟合时代
由于人类的自我优越感以及日月星辰东升西落的经验，让我们长期都认为地球是宇宙的中心。第一个比较系统提出地心说的人当属天文学家欧多克斯（Eudoxus，死于公元前347年左右），但他的地心说是非常粗糙的，以至于无法解释很多基本现象，如无法准确预言日食和解释行星逆行等。但亚里士多德接受了地心说，并且由于他在政治和科学上的权威，使地心说免去了夭折的命运。后来托勒密通过他的本轮，完善了地心说，使之延续到了16世纪。
20
Jan
《方程与宇宙》：三体问题和它的初积分(六)
By 苏剑林 | 2011-01-20 | 62145位读者 | 引用The Three Body Problem and its Classical Integration
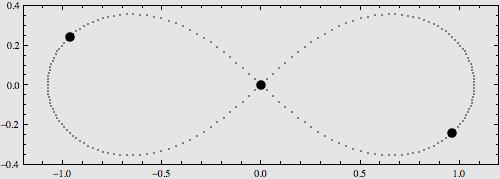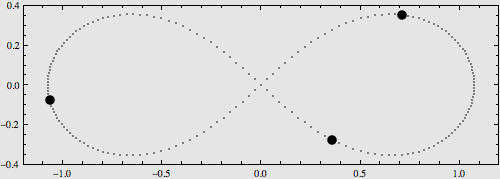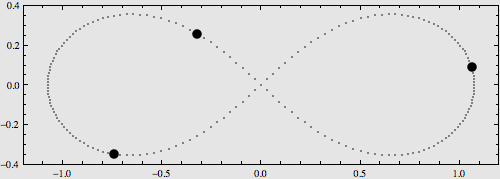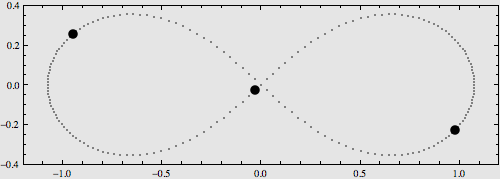
很多天文爱好者都已经接触到了“二体问题”（我们在高中学习到的“开普勒三定律”就是内容之一），由于在太阳系中行星质量相对较小而且距离相对较远，应用“二体问题”的解对天体进行计算、预报等能够满足一定的近似需求。不过，如果需要更高精度的计算，就不能把其他行星的引力给忽略掉了，于是就产生了所谓N体问题（N-Body Problem），即N个质点尽在它们各自引力的相互作用下的运动规律问题。最简单的二体已经被彻底解决，而三体或更多体的问题则与二体大相径庭，因为庞加莱证明了，三体问题不能严格求解，而且这是一个混沌系统，任何微小的扰动都会造成不可预期的效果。
根据牛顿力学，选择惯性参考系，设三个质点分别为$M_1,M_2,M_3$，向径分别为$\vec{r_1},\vec{r_2},\vec{r_3}$，可以列出运动方程（以下的导数都默认是对时间t求导）
9
Jan
不可能事件——一道经典电磁感应题的错误
By 苏剑林 | 2011-01-09 | 42275位读者 | 引用
19
Dec
N体问题的30个周期性解
By 苏剑林 | 2010-12-19 | 56093位读者 | 引用
28
Nov
《自然极值》系列——4.费马点问题
By 苏剑林 | 2010-11-28 | 86231位读者 | 引用通过上面众多的文字描述，也许你还不大了解这两个原理有何美妙之处，也或者你已经迫不及待地想去应用它们却不知思路。为了不至于让大家产生“审美疲劳”，接下来我们将试图利用这两个原理对费马点问题进行探讨，看看原理究竟是怎么发挥作用的。运用的关键在于：如何通过适当的变换将其与光学或势能联系起来。
费马点问题
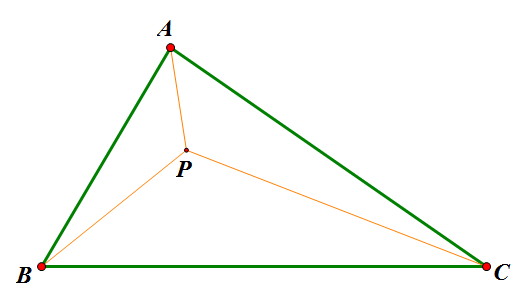
传统费马点问题是指在ΔABC中寻找点P，使得$AP+BP+CP$最小的问题；而广义的费马点则改成使$k_1 AP+k_2 BP+k_3 CP$最小。这是很具有现实意义的，是“在三个村庄之间建立一个中转站，如何才能使运送成为最低”之类的最优问题。我们将从光学和势能两个角度对这个问题进行探讨（也许有的读者已经阅读过了利用重力的原理来求解费马点，但是我想光学的方法依然会是你眼前一亮的。）
16
Aug
《方程与宇宙》:拉格朗日点,复数,向量(五)
By 苏剑林 | 2010-08-16 | 51237位读者 | 引用The New Calculation Of Lagrangian Point 4,5
上一回我们已经求出了拉格朗日点L1,L2,L3，并且希望能够求出L4,L5两个点。由于L4,L5与“地球-太阳”连线已经不共线了，所以前边的方法貌似不能够用了。为了得到一个通用的定义，我们可以采用以下方法来描述拉格朗日点：位于拉格朗日点的天体，它与太阳的连线以及地球与太阳的连线所组成的角的大小是恒定的。（这里为了方便，采用了地日系的拉格朗日点来描述，对于一般的三体问题是一样的）
对于L4,L5来说，我们或许可以设置一个新的向量来描述这两点的向径（如$\vec{R}$）。当我们这样做后，很快就会发现这样会令我们的计算走向死胡同。因为我们发现：已知两个向量的夹角和其中一个向量，我们很难把另一个向量用已知向量的式子表达出来。不能做到这一点，就不能找出$\vec{R}$与$\vec{r}$的关系，就无法联立方程求解。难道，我们这一条路走到尽头了吗？一开始BoJone也冥思苦想不得头绪，但是...
最近评论