在查找量子化有关资料的时候，笔者查找到了一系列名为《漫谈几何量子化》的文章，并进一步查询得知，作者为季候风，原来发表在繁星客栈（顺便提一下，繁星客栈是最早的理论物理论坛之一，现在已经不能发帖了，但是上面很多资料都弥足珍贵），据说这是除正则量子化和路径积分量子化外的第三种量子化方法。网上鲜有几何量子化的资料，更不用说是中文资料了，于是季候风前辈的这一十五篇文章便显得格外有意义了。
然而，虽然不少网站都转载了这系列文章，但是无一例外地，文章中的公式图片已经失效了，后来笔者在百度网盘那找到其中的十四篇pdf格式的（估计是网友在公式图片失效前保存下来的），笔者通过替换公式服务器的方式找回了第十五篇，把第十五篇也补充进去了。（见漫谈几何量子化（原文档）.zip）
虽然这样已经面前能够阅读了，但是总感觉美中不足，虽然笔者花了三天时间把文章重新用$\LaTeX$录入了，主要是把公式重新录入了，简单地排版了一下。现放出来与大家分享。
30
Jan
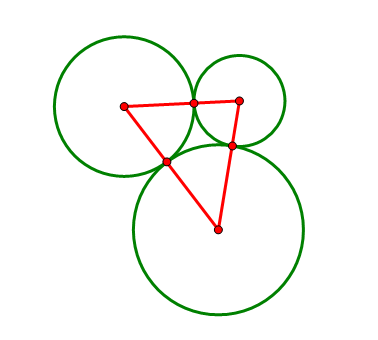
三个相切圆的公切圆:补充
By 苏剑林 | 2014-01-30 | 27108位读者 | 引用在学车的时候，我堂大哥曾问我一道作圆的问题：
三圆的外切圆和内切圆 (1)
平面上给出三个两两相切的圆以及它们的圆心，求作一个圆与这三个圆都相切（尺规作图）。
如果从纯几何的途径入手，我们甚至很难判断这样的圆是否存在。但是我之前似乎已经看过类似的题目，于是很快想到一个名词：反演。反演可以将圆反演成直线（圆过反演点），也可以将圆反演成圆（圆不过反演点），而其他的相切、相交等关系保持不变。对反演后的图形进行相同的反演，就变回原来的图形。本题的难点在于圆太多，利用反演，我们可以将它变为两条直线和一个圆的问题。
假设读者已经有了反演的基本知识，如果没有，请到
http://zh.wikipedia.org/wiki/反演
阅读相关内容。
11
Jan
几何的数与数的几何：超复数的浅探究
By 苏剑林 | 2014-01-11 | 59984位读者 | 引用这也是我的期末论文之一...全文共17页，包括了四元数的构造方法，初等应用等。附录包括行列式与体积、三维旋转的描述等。使用LaTex进行写作（LaTex会让你爱上数学写作的）
几何的数与数的几何
――超复数的浅探究
摘要
今天，不论是数学还是物理的高维问题，都采用向量分析为基本工具，数学物理中难觅四元数的影子。然而在历史上，四元数的发展有着重要的意义。四元数（Quaternion）运算实际上是向量分析的“鼻祖”，向量点积和叉积的概念也首先出现在四元数的运算中，四元数的诞生还标记着非交换代数的开端。即使是现在，四元数还是计算机描述三维空间旋转问题最简单的工具。另外，作为复数的推广，四元数还为某些复数问题的一般化提供了思路。
本文把矩阵与几何适当地结合起来，利用矩阵行列式$\det (AB) =(\det A)(\det B)$这一性质得出了四元数以及更高维的超复数的生成规律，并讨论了它的一些性质以及它在描述旋转方面的应用。部分证明细节和不完善的思想放到了附录之中。
26
Dec
高维空间的叉积及其几何意义
By 苏剑林 | 2013-12-26 | 59115位读者 | 引用向量之间的运算有点积和叉积（Cross Product，向量积、外积），其中点积是比较简单的，而且很容易推广到高维；但是叉积不同，一般来说它只不过是三维空间中的东西。叉积的难以推广在于它的多重含义性，如果将向量及其叉积放到张量里边来看（这属于微分形式的内容），那么三维以上的向量叉积是不存在的；但是如果只是把叉积看成是“由两个向量生成第三个与其正交的向量”的工具的话，那么叉积也是可以高维推广的，而且推广的技巧非常巧妙，与三维空间的叉积也非常相似。
回顾三维空间
为了推广三维空间的叉积，首先回顾三维空间的叉积来源是有益的。叉积起源于四元数乘法，但是从目的性来讲，我们希望构造一个向量$\boldsymbol{w}=(w_1,w_2,w_3)$，使得它与已知的两个不共线的向量$\boldsymbol{u}=(u_1,u_2,u_3),\boldsymbol{v}=(v_1,v_2,v_3)$垂直（正交）。从普适性的角度来讲，我们还希望构造出来的向量没有任何“奇点”，为此，我们只用乘法构造。至于叉积的几何意义，则是后话，毕竟，先达到基本的目的再说。
阿达马不等式
设有$n$阶实矩阵$\boldsymbol{A}=(a_{ij})_{n\times n}$，那么它的行列式满足阿达马(Hadamard)不等式
$$\begin{equation}
\left(\det \boldsymbol{A}\right)^2 \leq \prod\limits_{i=1}^{n}\left(a_{1i}^2+a_{2i}^2+\dots+a_{ni}^2\right)
\end{equation}$$
这是阿达马在1893年首先发表的。根据体积就是行列式的说法，上述不等式具有相当明显的几何意义。当$n=2$时，它就是说平行四边形的面积不大于两边长的乘积；当$n=3$时，它就是说平行六面体的体积不大于三条棱长的乘积；高维可以类比。这些结论在几何中几乎都是“显然成立”的东西。因此很难理解为什么这个不等式在1893年才被发现。当然，代数不会接受如此笼统的说法，它需要严格的证明。
25
Dec
《新理解矩阵5》：体积=行列式
By 苏剑林 | 2013-12-25 | 48767位读者 | 引用在文章《新理解矩阵3》：行列式的点滴中，笔者首次谈及到了行列式的几何意义，它代表了n维的“平行多面体”的“体积”。然而，这篇文章写于我初学矩阵之时，有些论述并不严谨，甚至有些错误。最近笔者在写期末论文的时候，研究了超复数的相关内容，而行列式的几何意义在我的超复数研究中具有重要作用，因此把行列式的几何意义重新研究了一翻，修正了部分错误，故发此文，与大家分享。
一个$n$阶矩阵$A$可以看成是$n$个$n$维列向量$\boldsymbol{x}_1,\boldsymbol{x}_2,...,\boldsymbol{x}_n$的集合
$$A=(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_n)$$
从代数的角度来看，这构成了一个矩阵；从几何的角度来看，这$n$个向量可以建立一个平行$n$维体。比如：平行四边形就是“平行二维体”，平行六面体就是“平行三维体”，高阶的只需要相应类比，不需要真正想象出高维空间的立体是什么样。
7
Jan
角的疑惑——为什么使用弧度？
By 苏剑林 | 2013-01-07 | 28411位读者 | 引用也许当我们从小学数学进入中学数学的过程中，让我们最郁闷的事情就是课本上把用的好好的角度制改为弧度制了，那个好好的360°的周角无端端变成了一个无理数$2\pi$，为此还多了一堆转换公式，那时这可把我折腾了好一阵子。为什么一个完美的360°不用，反而转向一个无理数$2\pi$？这里边涉及到了相当多的原因，在这些原因中，重新体现了数学体系的一致与简约。当然，文章里的观点只是我自己的看法，仅供大家参考。
弧度制：简约的要求
如果读者已经学过了极限理论，那么我就可以直接说，引入弧度制，是为了在这样的一种角的度量体制下，满足：
$$\lim_{x\to 0} \frac{\sin x}{x}=1$$
最近评论