27
Aug
科学空间：2011年9月重要天象
By 苏剑林 | 2011-08-27 | 14865位读者 | 引用秋高气爽的九月，天象剧场也逐渐热闹起来。秋分前后的夜晚，是一年中偶发流星出现最为频繁的时段。尤其是到了后半夜，如果赶上晴天，每小时看到二三十颗偶发流星都不成问题。与此同时，秋夜星空也不乏看点，美丽的仙女座星系M31肉眼可见，三角座星系M33等深空天体也是天文爱好者热衷的观测目标。除此之外，天王星将于本月迎来冲日，观测条件较好。
9月12日，我们又会迎来今年最重要的节日之一——中秋节。届时，不论您是身在他乡为“异客”，或是在家陪伴着亲人，BoJone都愿与你一起“举头望明月”。在此提前预祝大家中秋快乐、美满、团圆！
27
Jul
科学空间：2011年8月重要天象
By 苏剑林 | 2011-07-27 | 14948位读者 | 引用
8
Jul
均匀球状星团内恒星的运动
By 苏剑林 | 2011-07-08 | 15127位读者 | 引用我们考虑一个球状的星团，并假设它是各向同性的，即距离球心r处的物质密度ρ只与r有关，ρ=ρ(r)。那么，在半径为r的球形区域内的总质量为：
$$M(r)=\int_0^r 4\pi x^2 \rho(x) dx$$
想象有一颗质量比较小的恒星（其实相对于星团总质量，每一颗恒星的质量都很小）在星团的引力作用下运动（就好像太阳系绕着银河系运动一样），且恒星并没有受到其他物质（如星际尘埃等）的阻力。我们之前已经证明过，各向同性的球壳内部的引力是为0的，那么这种情况下的运动就相当于恒星只受到它到球心处的一个球形区域内的质量的引力吸引。根据万有引力定律，选择星团球心为参考系，可以得出
$$\ddot{\vec{r}}=-GM(r)\frac{\vec{r}}{r^3}$$
6
Jul
科学空间：2011年7月重要天象
By 苏剑林 | 2011-07-06 | 19907位读者 | 引用
28
May
科学空间：2011年6月重要天象
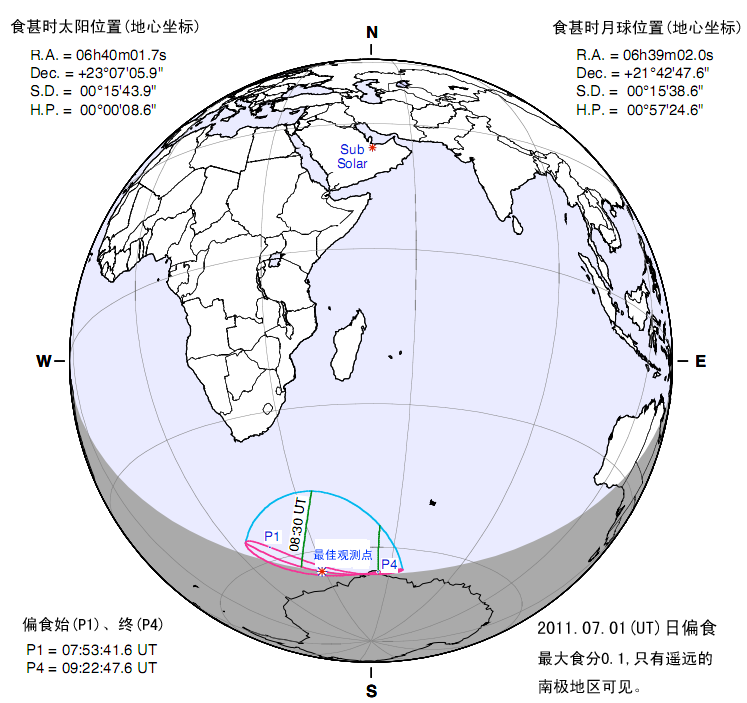
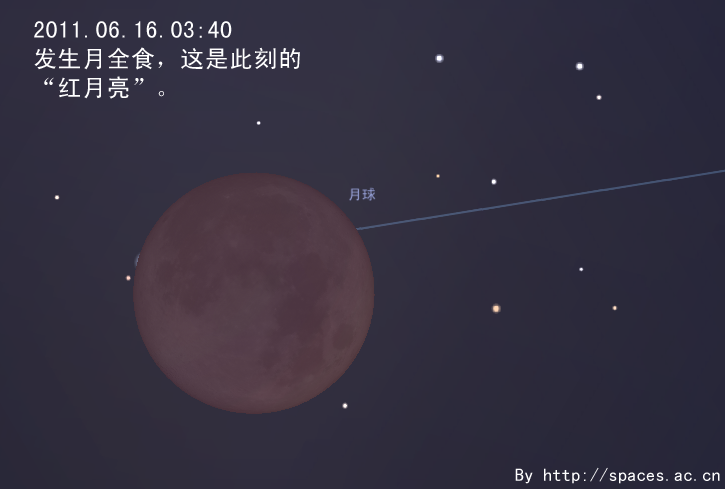
By 苏剑林 | 2011-05-28 | 22943位读者 | 引用
月全食-201106160340
6月中下旬，是北半球一年中黑夜最短的时期。今年6月22日是夏至节气，以北纬40°地区为例，当天天文昏影终到次日天文晨光始的间隔只有不到4小时50分钟。黑夜短暂会使我们可用于天文观测的时间缩短。但在夏至前后，午夜时分太阳也会在地平线下不太低的位置，这样我们就有可能整夜观测到一些类似国际空间站这样的低轨道人造天体。有兴趣的朋友可以查询相关的过境预报，挑战在一晚可以观测到多少次国际空间站过境这类的观测项目。发生在六月的日偏食和月全食，是今年天象的重头戏。接下来笔者就日偏食讲起，跟大家聊聊发生在6月的天象。
看完了“双不动中心”问题，我们不妨再来看一个貌似简单一点的力学问题，在一个固定质点的引力吸引的基础上，增加一个恒力作用，研究这样的力场中小天体的运动。
咋看上去这个问题比“双不动中心”简单多了，至少运动方程也显得更简单：
$$\ddot{vec{r}}=-GM\frac{\vec{r}}{|\vec{r}|^3}+\vec{F}$$
其中$\vec{F}$是一个常向量。不过让人比较意外的是，这个问题本质上和“双不动中心”是一样的，它可以看作是双不动中心问题的一个极限情况。而且它们的解法也是惊人地相似，下面我们就来分析这一个过程。
首先很容易写出这个方程的能量守恒积分：
$$1/2 \dot{vec{r}}^2-GM\frac{1}{|\vec{r}|}-\vec{F}\cdot \vec{r}=h$$
最近评论