SVD分解(一)：自编码器与人工智能

咋看上去，SVD分解是比较传统的数据挖掘手段，自编码器是深度学习中一个比较“先进”的概念，应该没啥交集才对。而本文则要说，如果不考虑激活函数，那么两者将是等价的。进一步的思考就可以发现，不管是SVD还是自编码器，我们降维，并不是纯粹地为了减少储存量或者减少计算量，而是“智能”的初步体现。

等价性 #

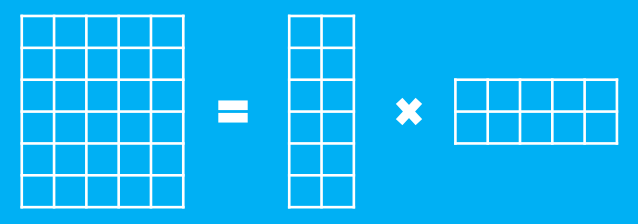
假设有一个$m$行$n$列的庞大矩阵$M_{m\times n}$，这可能使得计算甚至存储上都成问题，于是考虑一个分解，希望找到矩阵$A_{m\times k}$和$B_{k\times n}$，使得
$$M_{m\times n}=A_{m\times k}\times B_{k\times n}$$
这里的乘法是矩阵乘法。如图

这样本来有$mn$个元素，现在变成了右端的$(m+n)k$个元素，如果$k$足够小，那么就有$(m+n)k < mn$，这样使得存储量和计算量都降低了。当然，如果$k$足够小的话，那么等号一般不能严格成立，都是在误差最小的情况下成立，我们这里就不做严格区分了。这就是本文要描述的SVD分解（的核心）。如果$M_{m\times n}$这个矩阵本来是稀疏的（比如用one hot表示的文档矩阵、用户的评分矩阵），那么通常可以做到$k$小几个数量级，但精度基本不变。SVD的用途之一就是用来做主题模型、推荐系统等等。（注：可能有些地方的SVD不是这样定义的，但至少SVD的基本目的就是这样的。）

那么自编码器又是怎么回事呢？这里我们先无视激活函数，只看线性结构。自编码器是希望训练一个$f(x)=x$的恒等函数，但是中间层节点做了压缩。

数学公式看，就是希望找到矩阵$C_{n\times k}$和$D_{k\times n}$
$$M_{m\times n}=M_{m\times n} \times C_{n\times k}\times D_{k\times n}$$
这里的等号也不是严格相当，而是最优意义下的，图示如下：

这样一来，如果让
$$A_{m\times k} = M_{m\times n} \times C_{n\times k},\quad B_{k\times n} = D_{k\times n}$$
那么两者不就是等价了吗？只要它们在同一种误差函数（损失函数）下求最优得到的结果，那么所得到的结果必然是等价的。

这样子，我们就证明了，不带激活函数的三层自编码器，其实跟传统的SVD分解是等价的。但虽然是等价的，但自编码器还是一个创新，因为它将矩阵分解变为一个神经网络的压缩编码问题，更为清晰易懂，而且这样我们可以分批训练，不用像SVD那样要一次性把所有数据输入分解（当然，可以模仿神经网络的分批训练，来构思一个“分批SVD分解”算法，不过也没啥意义了。）

压缩与智能 #

虽然自编码器在压缩、编码上更为直观，但是SVD分解的物理意义更为明确。这表明从不同角度来看同一个东西是非常有意义的。SVD的物理意义可以这样观察，我们考虑一个文档编码，如下图所示，每一列代表一个词，每一行代表一篇文章，如下图就有A、B、C、D、E五个词，6篇文章的意思。

如图，SVD的物理意义，我们可以这样看。对于第一个分解的矩阵，我们可以看成是对行进行了聚类，即对文档进行了简单的聚类；第二个分解的矩阵，我们可以看成是对列进行了聚类，即对每个词语进行了聚类。而矩阵的乘法，就意味着文档类与词语类的匹配。读者可能会问为什么词语和文档要聚成相同数目的类？而不是不同数目的？事实上，更合理的写法是
$$M_{m\times n}=A_{m\times k}\times P_{k\times l} \times Q_{l\times n}$$
这样，就相当于说把文档聚为$k$类，词语聚为$l$类，$P_{k\times l}$就是文档类与词语类的匹配矩阵，然后将$P_{k\times l} \times Q_{l\times n}$设为$B_{k\times n}$就行了。

为什么要构思这样一种看似牵强的解释？笔者的目的，是去解释人工的模型中，体现出“智能”的原因是什么。我们知道，人有记忆功能，但记忆到一定程度之后，往往不会满足单纯的记忆了，而是找出要记忆的东西的规律，通过规律来记忆。比如在语言中，我们会将词语分为动词和名词，等等，然后我们发现“动词+名词”通常可以构成一个短语等规律，我们不一定说得出这个模式，但不可否认我们大脑确实在进行着这样的“找规律”、“分类”的过程，而这我觉得，如果用数据挖掘的角度来的话，就是一个压缩和聚类的过程，也就是说，通过压缩后进行重建，能够挖掘数据的共性，即我们所说的规律，然后得到更泛化的结果。

这或许可以回答一些问题，比如基于深度学习的（不论是LSTM还是CNN）的分词模型，为什么都对新词有那么好的识别能力？因为它里边包含了自编码器这个结构，而这个结构跟SVD等价，SVD我们前面解释了，含有了聚类这个物理意义（找规律），从而它更为泛化，性能更好。

衍生新词 #

太抽象？听不懂？不急，马上来一个例子。这个例子涉及到我们对词语的理解。请看下面的表格：
$$\begin{array}{c|c|c|c|c|c}
\hline
& \text{兽} & \text{界} & \text{龙} & \text{灵} & \text{术} \\
\hline
\text{神} & 1 & 1 & 1 & 1 & 0 \\
\hline
\text{魔} & 1 & 1 & 1 & 1 & 1 \\
\hline
\end{array}$$

假设这是一个从科幻小说中统计出来的结果，里边代表着“神兽”、“神界”、“神龙”、“神灵”、“魔兽”、“魔界”、“魔龙”、“魔灵”、“魔术”这些词都在小说中出现了，而且频数为1，但没有出现过“神术”这个词。那么我们是否会推理：“魔”跟“神”在用法上似乎有点相似，那么“神术”是不是成立的词？如何用数学表述这一点？

让人意外的是，做法之一正是SVD！也就是说，我们应该要对第一字的用法做一些聚类（可能是形容词、动词、名词？），对第二字的用法做一些聚类（可能是形容词、动词、名词？），然后考虑类与类之间的搭配。当然，我们不用真的告诉计算机要聚类为名词还是动词，计算机不需要用人类的方式去理解语言，我们只需要告诉计算机去聚类，而SVD正是有聚类这个含义，于是，只要做SVD就行了。具体实验如下：

将结巴分词的词表中所有频数不小于100的二字词选出来，然后以第一字为行，第二字为列，频数为值（没有这个词就默认记为0），得到一个矩阵。对这个矩阵做SVD分解，得到两个矩阵，然后把这两个矩阵乘起来（复原），把复原后的矩阵当作新的频数，然后对比原始矩阵，看看多出了哪些频数较高的词语。

结果，我得到了一些输入词表中没有的词语，比如（下面只是小部分）

龙脑 10.271244
龙脚 12.496673
龙腊 16.860170
龙腿 12.172765
龙莲 11.362767
龙蔗 67.800909
龙薯 30.580730
七讲 11.439969
七评 12.362163
七课 11.587767
七郎 12.789438
七隐 10.479609
七页 15.499356
七项 18.802959
怨怒 29.831461
怨恶 15.875075
怨苦 24.979326
怪兔 10.246062
怪奇 12.768122
怪孩 14.391967
怪形 14.856068

这些词语中，有不少是不靠谱的，事实上不靠谱的比靠谱的多得多。但这不重要，因为我们如果对自然语言进行处理的话，不靠谱的并不是真实环境中出现的句子。这就得到了很神奇的结果：我们通过SVD分解，原始的目的可能是压缩、降维，但复原后反而衍生出了更丰富、词汇量更多的结果。这似乎就是聚类、找规律的结果。这不同基于统计的新词发现，这些新词在语料中并不存在，是通过已有的词语的构造规律衍生出来的，是一个真正推理的过程，即“智能”。夸张地说，SVD带来了初步的人工智能（当然，不是唯一的方法）。

激活函数 #

激活函数是什么鬼？笔者在上面的实验中，也发现了激活函数的一个实在的物理意义。我们对矩阵做SVD分解，然后复原，复原后会有一些元素是负数的，而我们这个矩阵的含义是频数，频数不能是负数，因此我们把负数扔掉（截断），记为0。

咦？这不就是函数$\max(x,0)$的操作吗？这不是我们使用得最广的ReLu激活函数吗？原来，激活函数在这里的物理意义，不过是对无关紧要元素的一种舍弃（截断），这种操作，我们在很久之前的统计就已经用到了（扔掉负数、扔掉小统计结果等）。

当然，在神经网络中，激活函数有更深刻的意义，但在浅层的网络（矩阵分解）中，它给我们的直观感受，就是截断罢了。

小结 #

本文主要是以SVD为中心，探讨了SVD本身的物理意义（聚类）、SVD分解与自编码器的联系、SVD分解与智能的千丝万缕的关系以及一个相关实验。这些内容大多数是思想性的、理解性的，即加深我们对模型和人工智能的理解，是我们在运用模型中更有“底气”一些，而不是纯粹的套模型。

转载到请包括本文地址：https://kexue.fm/archives/4208

更详细的转载事宜请参考：《科学空间FAQ》