一维弹簧的运动(下)
By 苏剑林 | 2014-03-13 | 23202位读者 |在上一篇文章中,我们得到了一维弹簧运动的方程
$$m\frac{\partial^2 X}{\partial t^2}=k\frac{\partial^2 X}{\partial \xi^2}$$
并且得到了通解
$$X=F(u)+H(v)=F(\xi+\beta t)+H(\xi-\beta t)$$
或者
$$X(\xi,t)=\frac{1}{2}\left[X_0(\xi+\beta t)+X_0(\xi-\beta t)\right]+\frac{1}{2\beta}\int_{\xi-\beta t}^{\xi+\beta t} X_1 (s)ds$$
在文章的末尾,提到过这个解是有些问题的。现在让我们来详细分析它。
弹指神通
让我们用一个例子来演示一下上面的解,不妨设初始状态为
$$\xi=\left\{\begin{array}{} 0,x <0\\ \sin x,x\in[0,\frac{\pi}{2}] \\ 1 ,x > 0\end{array}\right.$$
反解得
$$x=\arcsin \xi$$
代入通解表达式
$$X(\xi,t)=\frac{1}{2}[\arcsin(\xi+\beta t)+\arcsin(\xi-\beta t)]$$
一切看起来都没有问题,但是上述解确实有不当之处的。注意,$\xi$的取值是0到1,比如我们考虑$\xi=1,t>0$,那么$\xi+\beta t>1$,此时$\arcsin(\xi+\beta t)$就不是实数了!可是好端端一个通解,怎么会出现这样的情况呢?
原因在于,当我们用对$\xi$的积分代替了求和时候,实际上使用了一个隐藏的假设:连续性!
也就是说,我们假设初始状态$x_i$位于$x_{i+1}$的左边,经过一段时间运动之后,$x_i$还是位于$x_{i+1}$的左边。这不一定成立,比如我们只考虑两个物体的弹簧,初始状态如下
其中$x_1$一端绷紧,而$x_2$一端被拉开,只要$x_2$到$x_1$的距离足够长,也就是远远超过了原长,那么释放之后,$x_1$向右运动,$x_2$向左运动,而我们的假设之中它们都是质点,没有碰撞这一概念,而且在我们的方程之中,两个质点只是被一个与距离平方成正比的势能联系着,并不是由一根具体的弹簧拉扯着,所以可以使得$x_2$在左边,$x_1$在右边,并且两者在一段时间内越来越远。这样子就破坏了连续性假设。在无限多个质点的情况也是类似的。
于是,总的来说,我们得到的“通解”,实际上只适合描写$0<\xi+\beta t<1,0<\xi-\beta t<1$这个区域内的运动。超出了这个区域,也就需要修改了。至于怎么修改,我也还在思考当中。
转载到请包括本文地址:https://kexue.fm/archives/2434
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Mar. 13, 2014). 《一维弹簧的运动(下) 》[Blog post]. Retrieved from https://kexue.fm/archives/2434
@online{kexuefm-2434,
title={一维弹簧的运动(下)},
author={苏剑林},
year={2014},
month={Mar},
url={\url{https://kexue.fm/archives/2434}},
}







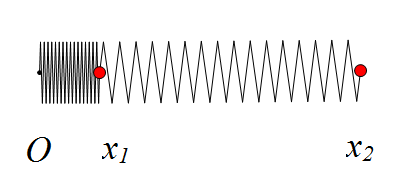



March 18th, 2014
超过这个区域,就有“碰撞”发生了,于是就不能视作质点了,于是就要考察弹簧本身的属性了,比如直径,杨氏模量,碰撞系数等等
我考虑过一个模型,就是它们同时还受到$\delta(x_i-x_{i-1})$的势能,这样子一旦碰撞,就立马反弹。想象中这样的模型应该可以成立的,估计可以给出适当的方程,但是我在数学上还不能描述它。