收谷问题(1)

在农村，7月是忙碌的月份，农民们要忙着收割稻谷，收割完后要晒谷，同时还得准备“下秧”，准备新一轮的耕，BoJone家自然也不例外。不过我家田比较少（1亩左右），收割机几分钟搞定，谷也三两天就晒完了。不过在晒谷的时候，BoJone在考虑一个“收谷”问题：

晒谷时得先把成堆的谷子摊开，薄薄地平铺在平地上，等到傍晚或即将下雨时（这是最惨的情况，搞不好会淋谷）就将其收起来。问题就源于这里，一般来说我们会把谷均匀地铺成矩形，要把所有的谷都推到矩形里或外的哪一点上，才使得我们做功做小？

这个问题还可以推广开来，例如对于一地任意形状的谷子（如三角形），把它集中堆到哪个点最“轻松”？一堆固定质量的谷子，要把它平铺成什么形状，才使得收谷时最“轻松”？当然，这个问题的解不仅仅用于“收谷”，在很多规划建设中也可以应用到，例如要在一个人口大致均匀的城市中建设一个服务中心，这个服务中心应该建在哪里？这有点类似于我们之前讨论过的费马点问题 ，都是费马点只考虑了三个点的距离，而这个问题得考虑所有点的距离。

事不宜迟，我们先看第一个问题：要把所有的谷都推到矩形里或外的哪一点上，才使得我们做功做小？其实由对称我们很容易就证明这个点就是矩形的几何中心（读者自己来试试？）。不过BoJone不满足于定性分析，我想进行一下定量的计算。

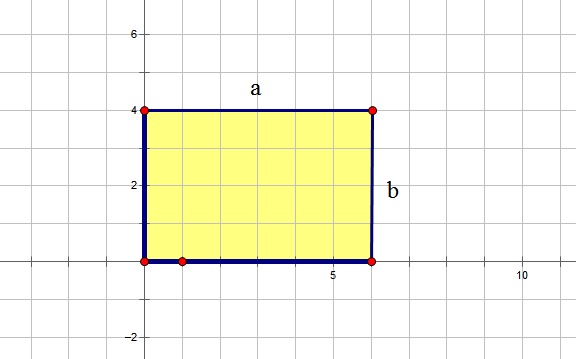
我们先来考虑把谷都堆到一个角（原点）上的情况。设谷的面密度为1，收谷做功应该与质量和距离都成正比，于是在矩形中一块边长分别为dx,dy的小矩形谷运回原点所做的功为$\sqrt{x^2+y^2} dxdy$，整块谷地运回原点所做的功应该是二重积分：
$$W=\int\int \sqrt{x^2+y^2}dxdy$$
（积分区域是一个边长为a,b的矩形）

这里为还没有接触过二重积分的朋友做个简介。二重积分的计算可以变成二次积分来积分，即先把y看成已知量，对x进行定积分运算，计算完后就把y当成变量，进行关于y的定积分运算。一重积分（就是我们平常接触的定积分）运算的积分区域是一条线（例如$\int_a^b f(x)dx$的积分区域是x轴上从a到b的一条线段），而二重积分的积分区域是一个平面，因此二重积分会比定积分复杂很多。例如在“先把y看成已知量，对x进行定积分运算”这一步时，要写出积分区域中x关于y的表达式，即定积分上下区间的差表示的是x关于y的表达式。

二重积分W可以直接进行计算，但是为了化简，我希望能够通过极坐标来进行变换：
$$W=\int\int r^2 dr d\theta$$

看起来是否简单多了？我们把$\theta$看成已知的，对r进行定积分。可是这里的积分区间怎么写呢？在图上可以看出在右下方的直角三角形区域，有$r=\frac{a}{cos\theta}$（即矩形最右的那条边的方程），于是积分区间可以写成$[0,\frac{a}{cos\theta}]$，即

$$W_1=\int(\int_0^{a//\cos\theta} r^2 dr)d\theta=\int(1/3 r^3|_0^{a//\cos\theta})d\theta=\int\frac{a^3}{\cos^3\theta} d\theta$$

根据这里，我们有

$$W_1=\frac{a^3}{4}(\frac{2\sin \theta}{\cos^2 \theta}+ln|\frac{1+\sin \theta}{1-\sin \theta}|)$$
其中$\theta=arctg(b/a)$。

可是这只是一半。左上方的一边积分等于：
$$\begin{aligned}W_2=\int(\int_0^{b//\cos\theta} r^2 dr)d\theta=\int(1/3 r^3|_0^{b//\cos\theta})d\theta=\int\frac{b^3}{\cos^3\theta} d\theta \\ =\frac{b^3}{4}(\frac{2\sin \theta}{\cos^2 \theta}+ln|\frac{1+\sin \theta}{1-\sin \theta}|)\end{aligned}$$
其中$\theta=arctg(a/b)$

其结果是不是已经让我们有点头晕了？是的，BoJone也头晕了，但是还是坚持下去吧。W可以写成：
$$\begin{aligned}\frac{a^3}{4}(\frac{2b\sqrt{a^2+b^2}}{a^2}+2ln|\frac{\sqrt{a^2+b^2}+b}{a}|)+\frac{b^3}{4}(\frac{2a\sqrt{a^2+b^2}}{b^2}+2ln|\frac{\sqrt{a^2+b^2}+a}{b}|) \\ =ab\sqrt{a^2+b^2}+1/2 a^3 ln|\frac{\sqrt{a^2+b^2}+b}{a}|+1/2 b^3 ln|\frac{\sqrt{a^2+b^2}+a}{b}|\end{aligned}$$

算是算出来了，但是如此繁琐的式子令我们不禁望而却步，这就要求我们另辟蹊径.....（待续）

转载到请包括本文地址：https://kexue.fm/archives/1439

更详细的转载事宜请参考：《科学空间FAQ》