双固定引力中心问题

我们在研究地球附近的小天体运动时，如果把天体和地球看作一个二体系统，那最多只能算上一个零级近似，如果使用“地球+月球+小天体”组成的圆形限制性三体问题模型，那可以算上一个二级近似了。那么，一级近似又是什么了。BoJone认为，它就是本文将要讲的“双固定引力中心问题”了，也叫“双不动中心问题”，英文名是two fixed-center problem。这是一种特殊的限制性三体问题。在这个三体系统中，两个主天体（或称有限质量天体）固定不动，第三个小天体在两个固定的主天体吸引下运动。欧拉、拉格朗日、勒让德、雅可比等人很早就研究过这个问题。其中，欧拉最先成功地求出了这个系统的积分。^[引用]

另外，双固定引力中心问题还有另外一个应用，在研究人造卫星的运动时，可以只考虑地球引力，但是由于地球不是完美的球体，把其看成一个质点其实不十分精确，要是把它拆分为两个引力源，就可以很大程度上提高精确度。毕竟双固定引力中心问题是完全可以积分的，可以作为一个比较好的中间轨道（介乎圆锥曲线和精确轨道之间的）。

只需要一点点力学分析知识，就不难列出双固定引力中心问题的运动方程（设所求运动物体的质量为1）：
$$\begin{equation}\ddot{\vec{r}}=-GM_1\frac{\vec{r}-\vec{d}}{|\vec{r}-\vec{d}|^3}-GM_2\frac{\vec{r}+\vec{d}}{|\vec{r}+\vec{d}|^3}\end{equation}$$

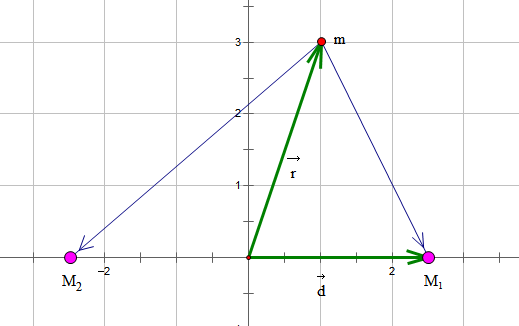
其中，选取的是两个固定的引力源的中心为原点，$\vec{d}$是$M_1$天体的位置向量。该方程有能量积分：
$$\begin{equation}\frac{1}{2} \dot{\vec{r}}^2-GM_1\frac{1}{|\vec{r}-\vec{d}|}-GM_2\frac{1}{|\vec{r}+\vec{d}|}=h\end{equation}$$

接下来我们只考虑平面情况，选取适当的长度单位使得$\vec{d}=(1,0)$，并且记$GM_1=\mu_1,GM_2=\mu_2$。该系统的动能为$T=\frac{1}{2} (\dot{x}^2+\dot{y}^2)$，势能为$U=-\frac{\mu_1}{\sqrt{x^2+y^2+1-2x}}-\frac{\mu_2}{\sqrt{x^2+y^2+1+2x}}$。能量守恒积分即
$$\begin{equation}T+U=h\end{equation}$$

而拉格朗日函数为$L=T-U$。接下来的关键是使用一个适当的坐标系把拉格朗日方程继续化简下去。欧拉天才地选择了椭圆坐标系，这可以在汪家訸的《三体问题》中看到。但是我们无法知道欧拉是怎样思考得到这个变换了。作为猜测，BoJone给出一个思考过程。由于势能U中含有两个根号，我们都不喜欢去处理有根号的东西。于是我们应当想办法进行适当的坐标变换消去两个根号。而根号里边的$(x^2+y^2+1-2x)$和$(x^2+y^2+1+2x)$除了一正一负外并无差别，这不禁让我们想到了公式$(a \pm b)^2=a^2+b^2 \pm 2ab$。那么，我们令$x=2ab,a^2+b^2=x^2+y^2+1$，从而解出
$$y^2=(a^2-1)(1-b^2)$$

又可以联想到$\cos^2\theta+\sin^2\theta=1,\cosh^2\varphi -1=\sinh^2\varphi$，因而可以考虑
$$\begin{aligned}x &=\cosh \varphi \cos \theta\\
y &=\sinh \varphi \sin \theta
\end{aligned}$$

这就是所希望的坐标变换。但是，如果我们是这样思考的话，我们并不能确定这样的变换对问题是否真的有帮助。但不论如何，我们应该做下去，因为即使错了，也是值得的，这会令我们更加深刻甚至有意外的发现。变换后的动能可以改写成：
$$T=\frac{1}{2} (\cosh^2 \varphi -\cos^2 \theta)(\dot{\varphi }^2+\dot{\theta}^2)$$
势能为
$$U=-\frac{\mu_1}{\cosh \varphi -\cos \theta}-\frac{\mu_2}{\cosh \varphi +\cos \theta}$$

能量积分是
$$\begin{equation}\begin{aligned}h&=T+U\\
&=\frac{1}{2} (\cosh^2 \varphi -\cos^2 \theta)(\dot{\varphi }^2+\dot{\theta}^2)\\
&-\frac{\mu_1}{\cosh \varphi -\cos \theta}-\frac{\mu_2}{\cosh \varphi +\cos \theta}\end{aligned}\end{equation}$$

拉格朗日方程是：
$$\frac{d}{dt}(\frac{\partial L }{\partial \dot{\varphi}})=\frac{\partial L }{\partial \varphi}$$

即
$$\begin{equation}\frac{d}{dt}[(\cosh^2 \varphi -\cos^2 \theta)\dot{\varphi }]=\cosh\varphi \sinh\varphi(\dot{\varphi }^2+\dot{\theta}^2)-\frac{\partial U }{\partial \varphi}\end{equation}$$

到这BoJone就没辙了。可是天才的欧拉却能够天才地想到这一步：各项乘上$(\cosh^2 \varphi -\cos^2 \theta)\dot{\varphi }$，就有

$$\begin{equation}\begin{aligned}&\frac{1}{2} \frac{d}{dt}[(\cosh^2 \varphi -\cos^2 \theta)^2 \dot{\varphi }^2]\\
=&(\cosh^2 \varphi -\cos^2 \theta) (\dot{\varphi }^2+\dot{\theta}^2)\cosh\varphi \sinh\varphi \dot{\varphi } \\
&-\frac{\partial U }{\partial \varphi}(\cosh^2 \varphi -\cos^2 \theta)\dot{\varphi}\end{aligned}\end{equation}$$

注意到右端有$(\cosh^2 \varphi -\cos^2 \theta) (\dot{\varphi }^2+\dot{\theta}^2)=2T$，于是可以写成
$$\begin{equation}\frac{1}{2} \frac{d}{dt}[(\cosh^2 \varphi -\cos^2 \theta)^2 \dot{\varphi }^2]\\
=2(h-U)\cosh\varphi \sinh\varphi \dot{\varphi } +\frac{\partial (h-U) }{\partial \varphi}(\cosh^2 \varphi -\cos^2 \theta)\dot{\varphi }\end{equation}$$

右端即
$$\begin{equation}\dot{\varphi}\frac{\partial }{\partial \varphi}[(h-U)(\cosh^2 \varphi -\cos^2 \theta )] \end{equation}$$

代入U的表达式，(8)还可以进一步化简：
$$\begin{equation}\dot{\varphi}\frac{\partial }{\partial \varphi}[(h(\cosh^2 \varphi -\cos^2 \theta )\\
+\mu_1(\cosh\varphi+\cos\theta)+\mu_2(\cosh\varphi-\cos\theta)] \end{equation}$$

$\varphi,\theta$是相互独立的，且$\theta,\varphi$部分已经相互分离了，含$\theta$的部分对$\varphi$的偏导数为0，因此(8)式子等价于
$$\begin{equation}\dot{\varphi}\frac{\partial }{\partial \varphi}[h \cosh^2 \varphi +(\mu_1+\mu_2)\cosh\varphi] \\=\frac{d}{dt}[(h \cosh^2 \varphi +(\mu_1+\mu_2)\cosh\varphi]\end{equation}$$

于是(6)式子变为
$$\begin{equation}\frac{1}{2} \frac{d}{dt}[(\cosh^2 \varphi -\cos^2 \theta)^2 \dot{\varphi }^2]\\=\frac{d}{dt}[(h \cosh^2 \varphi +(\mu_1+\mu_2)\cosh\varphi]\end{equation}$$

现在的可以两端积分了，有
$$\begin{equation}\frac{1}{2} (\cosh^2 \varphi -\cos^2 \theta)^2 \dot{\varphi }^2=h \cosh^2 \varphi +(\mu_1+\mu_2)\cosh\varphi+ C\end{equation}$$

由能量积分(4)可以变形得到
$$\begin{equation}\frac{1}{2} (\cosh^2 \varphi -\cos^2 \theta)^2 (\dot{\varphi }^2+\dot{\varphi}^2)\\
=h (\cosh^2 \varphi -\cos^2\theta)+(\mu_1+\mu_2)\cosh\varphi+(mu_1-\mu_2)\cos\theta\end{equation}$$

对比(12)就可以分离得到
$$\begin{equation}\frac{1}{2} (\cosh^2 \varphi -\cos^2 \theta)^2 \dot{\varphi}^2=-h \cos^2\theta+(mu_1-\mu_2)\cos\theta-C\end{equation}$$

用(14)除以(12)就得
$$\begin{equation}(\frac{d\theta}{d\varphi})^2=\frac{-h \cos^2\theta+(mu_1-\mu_2)\cos\theta-C}{h \cosh^2 \varphi +(\mu_1+\mu_2)\cosh\varphi+ C}\end{equation}$$

很快得到
$$\begin{equation}\int \frac{d\theta}{\sqrt{-h \cos^2\theta+(mu_1-\mu_2)\cos\theta-C}}=\int \frac{d\varphi}{\sqrt{h \cosh^2 \varphi +(\mu_1+\mu_2)\cosh\varphi+ C}}\end{equation}$$

两边都是可积形式，皆为椭圆积分。其实从复数的角度就很容易看出两边的积分其实是等价的。因为$\cosh x=\frac{e^x+e^{-x}}{2},\cos x=\frac{e^{ix}+e^{-ix}}{2}$，两者只相差了一个虚数单位i，两者的积分是很容易相互变换的。

至此，双固定引力中心问题完毕。由于我们只是寻求其求解过程，不需要实际应用测试（这部分工作通常交给计算机来完成），因此不需要把积分的形式都写出来。事实上也没有必要。因为用积分的形式表示微分方程的解也就已经足够了。更多的内容可以参考汪家訸的《三体问题》。

转载到请包括本文地址：https://kexue.fm/archives/1350

更详细的转载事宜请参考：《科学空间FAQ》