四次方程的根式求解(通俗版)
By 苏剑林 | 2009-09-06 | 39851位读者 |前些时间发表了三次方程的一般求解 ,并通过了维基百科链接到了这里来,想不到带来了很多的人气,看到大家还是比较需要这方面的资料的。在此之前曾经承诺过会把4次方程的求根公式也写出来,现在终于有时间了,就此一写,希望能够为大家带来帮助。
$$ax^4+bx^3+cx^2+dx+e=0(a!=0)$$
仍然是这两句话:网上的资料中,一是缺乏描述专业数学公式的相关程序(很多网站都是这样);二是语言过于专业,不能大众化(如维基百科)。如果一开始我就去看wiki,那么我保证我到现在还不能弄懂。
话说卡丹从塔塔利亚的口中得到了三次方程的求根公式之后,他又有了一个不平凡的遭遇。一天,一个叫“费拉里”的人成为了他家中的仆人。然而,这个“仆人”却表现出了高超的数学能力,因此,卡丹和费拉里的关系很快地从主仆关系转变为师生关系。通过听卡尔达诺讲课,学习了拉丁语、希腊语和数学,后来,还作出了一项空前的成就,那就是发现了“四次方程的根式求解方法”!
分析过程:
与卡丹的三次方程解法同出一辙,费拉里先把一般的四次方程
$ax^4+bx^3+cx^2+dx+e=0$,
通过设$y=x+{b}/{4a}$,变成关于y的四次方程
$y^4+py^2+qy+r=0$ ———(A)在这道方程中,增加一个额外的变量z,并作以下变换:
$(y^2+p+z)^2=(p+2z)y^2-qy+(p^2-r+2pz+z^2)$ ———(B)可以证明,(A)和(B)等价。
如果我们可以把(B)的右边也变成完全平方形式,那么原方程就可以变成关于y的一元二次方程了。究竟怎样才能够把(B)的右边变成我们希望的完全平方形式呢?这取决于z。
我们知道,如果存在一道二次三项式$ax^2+bx+c(a!=0)$,使得这一道二次三项式为完全平方式的充分条件为$b^2-4ac=0$。而(B)右端正是这样的一条二次三项式,因此我们不妨令
$q^2-4(p+2z)(p^2-r+2pz+z^2)=0$ ———(C)那么就实现了我们的目的,而(C)是关于z的三次方程,是可以求解的。这样,我们求出了z后,可以把(B)两端同时开方,变为关于y的两道二次方程。这样可以求出4个y(一般情形),进而求出4个x。
因此,根式求解4次方程的一般步骤为:
1. 通过设$y=x+{b}/{4a}$,变成关于y的四次方程$y^4+py^2+qy+r=0$。
2. 解方程$q^2-4(p+2z)(p^2-r+2pz+z^2)=0$。
3. 解方程$(y^2+p+z)^2=(p+2z)y^2-qy+(p^2-r+2pz+z^2)$
4. 解方程$y=x+{b}/{4a}$。
可以想象,四次方程一般情形的求根公式会有多么的复杂!因此,似乎还没有这样的能人把这条公式写出来(或者说没有人愿意去写)!只是借助计算机写了出来
一元4次方程的4个根:
(1)
(2)
(3)
(4)
可以参考下:
http://planetmath.org/encyclopedia/QuarticFormula.html
http://www.wolframalpha.com/input/?i=a+x%5E4%2Bb+x%5E3%2Bc+x%5E2%2Bd+x%2Be+%3D+0
最后,现在看来,卡丹这个“伯乐”发现了费拉里这匹“千里马”,使得他能够在数学上绽放光彩!
转载到请包括本文地址:https://kexue.fm/archives/114
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Sep. 06, 2009). 《四次方程的根式求解(通俗版) 》[Blog post]. Retrieved from https://kexue.fm/archives/114
@online{kexuefm-114,
title={四次方程的根式求解(通俗版)},
author={苏剑林},
year={2009},
month={Sep},
url={\url{https://kexue.fm/archives/114}},
}









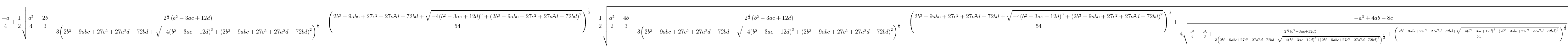




最近评论