《自然极值》系列——5.最速降线的故事

如果说前面关于这个系列的内容还不能使得读者您感到痛快，那么接下来要讲述的最速降线和悬链线问题也许能够满足你的需要。不过在进入对最速降线问题的理论探讨之前，我们先来讲述一个发生在17世纪的激动人心的数学竞赛的故事。我相信，每一个热爱数学和物理的朋友，都将会为其所振奋，为其所感动。里边渗透的，不仅仅是一次学术的竞争，更是一代又一代的人对真理的追求与探路的不懈精神。

（以下内容来源于网络，科学空间整理）

意大利科学家伽利略在1630年提出一个分析学的基本问题── “一个质点在重力作用下，从一个给定点A到不在它垂直下方的另一点B，如果不计摩擦力，问沿着什么曲线滑下所需时间最短。”这算是这个著名问题的起源了（为什么别人没有想起这个问题呢？所以说大科学家的素质就是思考、创新，要有思想，人没有思想，就和行尸走肉没有什么区别）。可惜的是伽利略说这曲线是圆，但这却是一个错误的答案。

瑞士数学家约翰·伯努利在1696年再次提出这个最速降线的问题（problemofbrachistochrone），向全欧洲数学家征求解答。伯努利将此问题称为Brachistochrone，即希腊语中的“最短”（brochistos）和“时间”（chronos）合成而来。

人们当然会首先想到连接AB的直线。伯努利说了：“虽然AB间线段最短，但小球滚下来的时间不是最短。如果在年底前（指1696年）没有人发现这条曲线，我将公布这条曲线。”直线有可能不是最短时间的路径，因为小球从零速度开始滚下来，最初应该让路径陡一些，好更快地加速获得速度。

这有点像武侠小说中的挑战了，显然，伯努利自己是得出了答案，才敢下此战书的。这个问题的难点在于，是求出一条曲线，实际就是求一个满足给出条件的未知函数，这在以前是前所未有的，有可能开创一个新的学科领域。于是数学家们具有极大兴趣，纷纷开展研究。

伯努利原定的截止期限是1696年年底，可是他只受到了一份解答，就是他的老师莱布尼兹（微积分的一个独立发明人，也是个大数学家），莱布尼兹要求伯努利将截止期限延长到来年复活节（大致在3月下旬到4月下旬之间），以便让欧洲数学家们有更多时间来充分解决此道难题。

有意思的是，伯努利在“战书”中还特别暗示了他的挑战对象，他写道：“……很少有人能解出我们的独特的问题，即使那些自称通过特殊方法……不仅深入探究了几何学的秘密、而且还以一种非凡的方式拓展了几何学领域的人，这些人自以为他们的伟大定理无人知晓，其实早已有人将它们发表过了”

这简直是赤裸裸的指向伟大的伊萨克·牛顿了！伯努利提到的“定理”显然是指流数术（牛顿自己给微积分起的名字），而牛顿曾宣称自己早在莱布尼兹1684年发表微积分论文前就已经发现了这一理论。前文说过，莱布尼兹正是伯努利的老师，自己师父和牛顿争夺微积分的发明权，弟子当仁不让要维护师门尊严。约翰·伯努利亲自把降速问题抄了一份，装进信封寄往英国（牛顿）。

此时牛顿已不是当年的牛顿了，他自己也承认，他的头脑已经不如二十年前那么机敏了，而且还整天忙于造币局的凡俗事务。关于此事我们可以看看牛顿的外甥女凯萨琳记述的内容：“1697年的一天，收到伯努利寄来的问题时，伊萨克牛顿爵士正在造币局里忙着改铸新币的工作，很晚才精疲力竭地回到家里。但是，直到解出此道难题，他才上床休息，这时已经是凌晨4点钟。”

即使是在晚年，而且忙了一天的本职工作，牛顿还是用几个小时就解决了许多欧洲数学家都无法解出的难题！这位伟大天才的功力可见一斑。牛顿感到了自己最为一代宗师的荣誉和名望都受到了挑战，对手正等着看他笑话，因此牛顿当仁不让，仅用几个小时就解决了此题。牛顿被激怒了，据说他说过：“在数学问题上，我不喜欢……被外国人……戏弄”。（当然，你要没有实力，只能被人戏弄）

1697年复活节的截止期限，伯努利共收到了5份答案，他自己和其老师莱布尼兹，第三份是他的哥哥雅可布·伯努利，这肯定使得约翰·伯努利很不爽，因为他们兄弟两个从来都是谁也不服谁，互相较劲。罗毕达是第四个。最后一份答案的信封上盖着英国的邮戳，有意思的是，竟然是匿名的，但答案完全正确！显然这封信来自一位绝顶天才，非伊萨克·牛顿莫属。据说，伯努利半是恼怒，半是敬畏地放下这封匿名答案，会意地说：“我从他的利爪认出了这头狮子。”

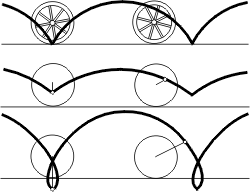
除了罗毕达的答案外，其他人的解答都在1697年5月5月的《博学通报》公布。答案就是一段旋轮线（摆线），帕斯卡和惠更斯以前就研究过这一重要的曲线，可是他们谁也没有想到这还是一条最速降线。因为钟表摆锤作一次完全摆动所用的时间相等，所以摆线又称等时曲线。

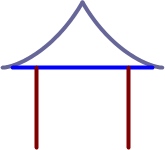
最速降线在建筑中也有着美妙的应用。我国古建筑中的“大屋顶”，从侧面看上去，“等腰三角形”的两腰不是线段，而是两段最速降线。按照这样的原理设计，在夏日暴雨时，可以使落在屋顶上的雨水，以最快的速度流走，从而对房屋起到保护的作用。

数学历史上的挑战古已有之，但这一次最速降线的挑战可谓数学史上最激动人心的一次挑战，有几个理由：

首先参与人数众多。其次，得出正确结果的都是赫赫有名的大数学家。牛顿、莱布尼兹各自独立创立了微积分；以伯努利兄弟为代表的伯努利家族是数学世家，其地位有点像音乐世家的巴赫家族。罗毕达年轻时就显露了数学天赋，十五岁就解出了帕斯卡的摆线难题（现在小升初的牛孩们距离15岁还有几年）。赫赫有名的罗毕达法则，大家学到高等数学就会耳熟能详。

第三，这次挑战各人的解法各有千秋，约翰伯努利的解法最漂亮，类比了费马原理，将物理和几何融合到一起，用光学的思想一下子就得出结论（有点像奥数的“杂耍”哈）。雅各布的方法最一般化，体现了变分思想。牛顿、莱布尼兹和罗毕达都是用微积分方法（相对于变分，微积分算“传统”方法了），但是步骤也不相同。

动画演示：

最后，此问题直接导致了另一位旷世天才的登场，大数学家莱昂哈德·欧拉（约翰·伯努利的学生）也在1726年开始发表有关的论著，1728年开始以他特有的透彻精神重新考察了最速降曲线等问题，最终确立了求积分极值问题的一般方法。欧拉的方法后来又为拉格朗日所发展，拉格朗日首先将变分法置于分析的基础上，他还充分运用变分法来建造其分析力学体系，全部力学被他化归为一个统一的变分原理——虚功原理。

这些新的分支与微积分本身一起，形成了被称之为“分析”的广大领域，与代数、几何并列为数学的三大学科，在十八世纪，其繁荣程度远远超过了代数与几何。

十八世纪的数学家们不仅大大拓展了分析的疆域，同时赋予它与几何相对的意义，他们力图用纯分析的手法以摆脱对于几何论证的依赖，这种倾向成为十八世纪数学的另一大特征，并且在欧拉和拉格朗日的工作中表现得最为典型。

拉格朗日在《分析力学》序中宣称：“在这本书中找不到一张图，我所叙述的方法既不需要作图，也不需要任何几何的或力学的推理，只需要统一而有规则的代数(分析)运算”。

转载到请包括本文地址：https://kexue.fm/archives/1094

更详细的转载事宜请参考：《科学空间FAQ》